A kötet a tetraéder - általános képletű, példák a számítás, számológép
Tekintsünk egy tetszőleges ABC háromszög, a D ponton nem síkjában a háromszög. Csatlakoztassa szegmenseit ezen a ponton a csúcsai a ABC háromszög. Ennek eredményeképpen megkapjuk a háromszög ADC. CDB. ABD. Által határolt felület négy háromszög ABC. ADC. CDB és ABD nevezzük tetraéder, és jelöljük DABC.
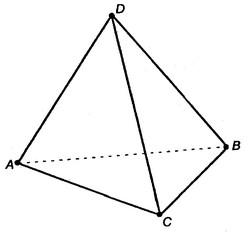
háromszög adatok felek nevezik szélei tetraéder. És a felsők - felsők tetraéder
A tetraéder négy arca. 6 élek és 4 csúcsa.
Két élek, amelyek nem rendelkeznek a közös vertex, az úgynevezett szemben.
Gyakran előfordul, hogy a kényelem, az egyik az arcok egy tetraéder nevezzük bázis. és a maradék három oldalát az oldalsó élek.
Így a tetraéder - a legegyszerűbb poliéder, akiknek az arca négy háromszög.
De az is igaz az állítás, hogy tetszőleges háromszög piramis a tetraéder. Aztán az is igaz, hogy egy tetraéder nevezzük piramis, amelynek alapja egy háromszög.
Magassága a tetraéder nevezzük szegmens, amely összeköti a felső lévő pontig a szemben lévő oldalfelületen, és a rá merőleges.
Medián tetraéder nevezzük szegmens, amely összeköti a felső, hogy a metszéspontja a medián az átellenes oldalára.
Bimedianoy tetraéder nevezzük szegmens, amely összeköti a közepén ferde élei a tetraéder.
Mivel a tetraéder - egy piramis egy háromszög alakú alap, a térfogata minden tetraéder lehet kiszámítani a következő képlettel
,
- S - területe minden arc,
- H - magasság, esett a szélén
Szabályos tetraéder - egy különleges formájú tetraéder
Tetraéder, amelynek minden részletét egy egyenlő oldalú háromszög nevezzük szabályos.
Az ingatlan egy szabályos tetraéder:
- Minden arcok egyenlő.
- Minden sík szöge szabályos tetraéder egyenlő 60 °
- Mivel minden csúcsa egy csúcs három egyenlő oldalú háromszög, az összeget a sík szögek minden csúcsa 180 °
- Minden csúcs egy szabályos tetraéder vetített átellenes oldalán orthocenter (metszéspontja magasságtól háromszög).
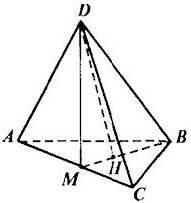
Legyen adott egy szabályos tetraéder ABCD élei egyenlő egy. DH - magassága.
Végzünk további konstrukciók BM - a magassága az ABC háromszög és a DM - magassága ACD háromszög.
Magasság BM és BM egyenlő
Tekintsük BDM háromszög. ahol DH. amely szintén a magasság a tetraéder és a magassága a háromszög.
Triangle magassága csökkentette oldalán a MB megtalálható az alábbi képlet segítségével
, ahol
BM =, DM =, BD = a,
p = 1/2 (BM + BD + DM) =
Behelyettesítve ezeket az értékeket az általános képletű magassága. megkapjuk
Olvasztott 1 / 2a. megkapjuk
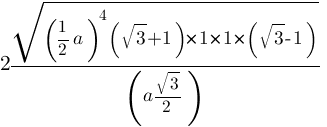
Alkalmazzuk a különbség négyzetek formula
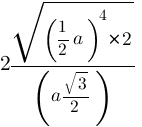
Miután néhány átalakulások megkapjuk
A kötet a bármely tetraéder lehet kiszámítani a következő képlettel
,
ahol
Behelyettesítve ezeket az értékeket, kapjuk
Így a képlet a kötet egy szabályos tetraéder
élű, ha a tetraéder
Térfogatának kiszámításához egy tetraéder, ha valaki ismeri a koordinátáit a csúcsok
Tegyük fel, hogy adottak a csúcsainak koordinátáit egy tetraéder
A felsők vektorok ,.
Ahhoz, hogy megtalálja a koordinátáit ezen vektorok kivonni a koordinátákat a végének megfelelő koordináta eredetű. megkapjuk
A geometriai jelentése a vegyes termék három vektor a következő - a kapott termék a három vektor egyenlő a térfogatának a paralelepipedon épített ezeket a vektorokat.
Mivel a tetraéder egy piramis, háromszög alap, és a térfogata a gúla hatszor kisebb, mint a doboz, akkor van értelme a következő képlet
Hogy megszilárdítsa az anyagot azt jelenti például a következő képlet segítségével térfogata a tetraéder.
A kötet a szabályos tetraéder egyenlő 2 cm 3. Keresse a kötet egy szabályos tetraéder, a szélén amely 3-szor több élén a tetraéder.
A kötet a szabályos tetraéder számítják az alábbi képlet szerint
majd
Fejezzük oldalán a kocka
Ha a felek, hogy növelje 3-szor, hogy a kocka, hogy növelje 27-szeres. majd
m
Találunk a hangerő
- A háromszög területe három oldalról

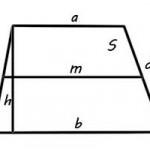
- A terület trapéz
- terület egy kör

- A háromszög területe a sugara a beírt kör

- A sugár a beírt kör pasztilla
