A relativitás elve Einstein és a Lorentz-transzformációk - studopediya

Az egyik legfontosabb fizikai állandói a fény sebessége vákuumban, vagyis a sebessége elektromágneses hullámok terjedését szabad térben az anyagról. Ez sebesség nem függ a frekvencia az elektromágneses hullámok, és ez ma már elfogadott, Az értékek egyenlő C = 299792458 m / s.

A esetek túlnyomó többségében ezt az értéket egy megfelelő pontossággal lehet venni, mint c = 3 • 108 m / s - ahol a hiba kisebb, mint 0,001.

És ez a „háromszázezer kilométer másodpercenként” a fény sebessége emlékeznek a legtöbben az élet. Emlékezzünk vissza, hogy a 300 000 km - a nagyságrend, a távolság a Föld a Hold (pontosabban 380 000 km).

Így a rádió jel eléri a földet a Hold, míg valamivel több, mint egy másodpercig.

Az a feltételezés, hogy a fény nem végtelen, hanem véges sebességgel beszélt évszázadokon emberek előtt tudták bizonyítani, hogy kísérletileg. Ez elsőként a XVII században, amikor csillagászati ​​megfigyelések furcsa „szabálytalanságokat” Jupiter műholdas Io mozgását is magyarázható csak a feltételezés egy véges terjedési sebessége a fény (mellesleg ez az első kísérlet arra, hogy meghatározza a fény sebessége adott alacsonyabb eredményt

Ez szerelt meglepő tény - az érték a fény sebessége nem függ attól, hogy kapcsolatban, hogy a referencia rendszer, ez határozza!

Ez a kísérleti tény ellentmond a törvény hozzáadásával sebességgel Galileo, amit arra az előző fejezetben és nyilvánvalónak tűnik, és megerősítették a napi megfigyelések. De a fény nem vonatkozik ez a természetes, látszólag sebesség szabályból - tekintetében minden megfigyelő, nem számít, hogyan mozogtak, a fénysugár azonos sebességgel c = 299793 km / s. És az a tény, hogy a fény terjedési - a mozgás az elektromágneses mező nem részecskék,

álló csoport, nem játszik szerepet itt. A levezetése sebesség kívül törvény (9.2) nem számít a természet a mozgó tárgyat.

És bár ez lehetetlen találni ilyet a korábbi felhalmozott tudás és tapasztalat, viszont el kell ismernünk, ezt a tényt a tapasztalat, emlékezve arra, hogy ez az élmény meghatározó kritérium az igazság. Emlékezzünk arra, hogy állunk szemben hasonló helyzetben az elején a kurzus, ha beszélünk a tulajdonságait helyet. Aztán megjegyezte, hogy elképzelni görbülete háromdimenziós térben, mi - a háromdimenziós lények -nevozmozhno. De rájöttünk, hogy az a tény, hogy „jelenléte vagy hiánya” görbületi lehet beállítani empirikusan: mérésével, például, az összeget egy háromszög szögei.

Milyen változásokat kell tenni, hogy megértsük a tulajdonságok a tér és idő? És a fény ezen tények az az átalakulás Galileo? Van-e lehetőség változtatni őket úgy, hogy még mindig nem ütköznek a józan ész, amikor használjuk a szokásos mozgását szervek körül minket, és ugyanakkor nem mond ellent az a tény, az állandóság, a fény sebessége minden referencia képkocka?

Az alapvető megoldás ezekre a problémákra tartozik Albertu Eynshteynu, aki megalkotta az elején a XX század. speciális relativitáselmélet (SRT) kapcsolatos szokatlan a fény terjedését az alapvető tulajdonságai a tér és idő, megnyilvánuló sebességgel összemérhető a fény sebességét. A modern fizikai irodalomban gyakran nevezik egyszerűen csak a relativisztikus mechanika.

Ezt követően épített Einstein általános relativitáselméletet (GTR), ahol az összefüggés tulajdonságok és a tér-idő gravitációs kölcsönhatás.

Az alapot a töltőállomás két kívánságot. amelyek úgynevezett Einstein relativitás elve és az elv a állandóságának a fénysebesség.

Einstein relativitás elve általánosítása elvének galileai relativitás tárgyalt az előző fejezetben, kivétel nélkül (nem csak mechanikai) természeti jelenségek. Ezen elv szerint, minden a természet törvényei ugyanazok minden inerciális referencia rendszereket. Einstein relativitáselmélete elve a következőképpen foglalható össze: minden az egyenlet természet törvényei invariáns tekintetében átalakulások koordináták és időt egy inerciális vonatkoztatási rendszer a másikra. (Emlékezzünk, hogy az invariancia

egyenletek úgynevezett változhatatlansága fajok helyett bennük a koordinátákat és az idő koordinátái hivatkozási rendszert, és a többi időben). Egyértelmű, hogy összhangban a relativitás elve, Einstein nem kísérletek egyáltalán nem lehet telepíteni, hogy mozog a „mi” vonatkoztatási rendszer állandó sebességgel, vagy álló helyzetben, vagy pontosabban, nincs különbség ezekben az országokban. Galileo feltételezték, hogy lehetetlen elvileg csak a mechanikai vizsgálatok.

állandóságának elve (pontosabban invariancia) a fénysebesség kimondja, hogy a fénysebesség vákuumban ugyanaz minden inerciális referencia rendszereket. Mint hamarosan látni fogjuk, az következik, hogy - a legnagyobb az összes lehetséges fizikai sebességek.

Mindkét posztulátumok tükrözi tapasztalati tények: a fénysebesség független a mozgás a forrás vagy a vevő; Ugyancsak nem függ a mozgás a referencia képkocka, amelyben a kísérleteket végeztünk annak mérése. A relativitás elve tükröződik az elismerést a tény, hogy nem csak a mechanikus, hanem az elektromágneses (fényeloszlás) jelenségek, engedelmeskedik minden inerciális referencia rendszerek

ugyanaz a törvényeket.

A fent megállapított rendelkezések magában foglalja számos fontos következtetéseket tulajdonságaival kapcsolatos térben és időben. Először is, követik az új szabályok az átmenet az egyik tehetetlenségi vonatkoztatási rendszer egy másik, ahol a „nyilvánvaló” Galilei-transzformáció csak néhány különleges esetekben, végre csak sebességgel haladó sokkal kisebb, mint c. Annak megállapításához, ezeket az új szabályokat fogja vizsgálni fény szaporítóanyag egy pontban elején található a fix rendszer referencia K (ábra. 10.1 a).

A fény terjedése lehet leírni terjedési fény elől, amelynek az alakja egy gömbfelület a referencia képkocka, amelyhez képest a fényforrás stacionárius. De a relativitás elve, Einstein első lámpa legyen gömbölyű, és akkor is, ha figyelünk a referenciakeret, amely egységes egyenes vonalú mozgás képest a forrás.

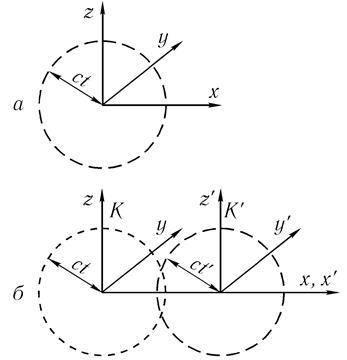
Ábra. 10.1 Fény szaporítóanyag egy pontszerű forrásból elején található az álló referencia képkocka, hogy az első a fény, hogy gömb alakú, és akkor is, amikor azt állapítják meg a referencia képkocka, amely egységes egyenes vonalú mozgás képest a forrás.

Ez a feltétel most meghatározni, mi legyen a szabályok átalakítására koordináták és az idő az átmenet az egyik tehetetlenségi rendszerből a másikba.

Ha a fényforrás található elején a referencia képkocka K, a kibocsátott fény a t = 0 időpontban, az egyenlet a gömb alakú fény-front a formája

x 2 + y 2 + z 2 = (ct) 2 (10.1)

Ez az egyenlet egy gömb alakú felület, amelynek sugara r = ct

Idő növekszik sebességgel.

Koordinátái és az idő által mért megfigyelő a mozgó keret K „jelöljük a prímszám betűk x”, y „z”, t”. Tegyük fel, hogy a start időzítése t „ideje egybeesik a kerettel t, és hogy a nulla időpont egybeeső felső K1 koordinátarendszerben egybeesik a helyzetét a fényforrás a rendszerben K. Ahhoz, hogy specifikus, a rendszer K” mozog a + x irányban állandó sebességgel V között K (ábra. 10.1 b).

Ahogy már mondtuk, szerint a második posztulátum Einstein, a megfigyelő az „alapozás” első lámpa rendszer szintén gömb alakú, vagyis az egyenlet a fény előtt a mozgó rendszer legyen a forma

x '2 + y' 2 ​​+ z '2 = C 2 t' 2 (10.2)

ahol a fény sebessége mennyiség itt ugyanaz azzal, hogy a keretben K. Ezért átalakulása koordinátáit és az idő a mi audio keret másik szükség, hogy rendelkezzen egy ilyen tulajdonság, hogy például a csere után ezekkel transzformációk (10.2) " alapozás „értékeket a” nem alapozott „megint csak fel kell szerezni az egyenlet a gömb alakú elülső (10,1).

Ez könnyen ellenőrizhető, hogy a Galilei-transzformáció (9.3) nem felel meg ennek a követelménynek. Emlékezzünk vissza, hogy ezek az átalakulások kapcsolódnak a koordinátákat és az időt két különböző referencia-keret a következő összefüggések:

x '= x - Vt, y' = y, Z '= Z, t' = t. (10.3)

Ha helyettesíteni (10,3) a (10.2), megkapjuk

x 2 - 2xVt + V 2 t 2 + y 2 + z 2 = C 2 t 2. (10.4)

ami persze, hogy nem felel meg az egyenlet (10,1). Mi, akkor kell, hogy legyen egy új megtért? Először is, mivel minden rendszer egyenlő, az átmenet a rendszer bármely más kell leírni ugyanazokat a képleteket (annak értéke V), egy két-szeres alkalmazása a transzformációk a csere a második lépés a + V

-V vissza kell nekünk az eredeti rendszer. Ez a tulajdonság lehet, hogy csak a lineáris függvényt x és t átalakulás. Hiába, hogy teszteljék ez a kapcsolat típusa

x „= x L / 2 t 1/2. x „= sin x

vagy hasonlók.

Másodszor, amikor V / s -> 0, az átalakulás kell mozgatni a Galileo átalakulás, amely érvényes az alacsony sebesség nem lehet megkérdőjelezni.

Egyenlet (10.4) egyértelmű, hogy nem hagyhatjuk megváltoztatása nélkül az átalakulás t „= t, ha azt akarjuk, hogy elpusztítsa ezt az egyenletet nem kívánt kifejezések -2xVt + V 2 t 2, mert pusztítani őket, akkor meg kell bizonyosodni arról, hogy adjunk valamit a t .

Próbálja első átalakítása az űrlapot:

x '= x-Vt, y' = y, Z '= Z, t' = t + bx, (10.5)

ahol b - állandó, amelynek értéke alapján kell meghatározni. Ezután egyenlet (10.2) formájában

x 2 - 2Vxt + V 2 t 2 + y 2 + z 2 = C 2 t 2 + 2c 2 BXT + c 2 b 2 x 2 (10.6)

Vegye figyelembe, hogy a feltételeket a bal és jobb oldalán az egyenlet a terméket tartalmazó xt, kioltják egymást, ha figyelembe

b = -V / c 2. vagy t „= t-Vx / c 2 (10.7)

Ezen érték b, egyenlet (10.6) lehet újraírni az alábbiak szerint:

2 x (1 - V 2/2) + y 2 + z 2 = C 2 t 2 (l - V 2/2). (10.8)

Ez közelebb áll az egyenlet (10.1), de még mindig marad egy nemkívánatos faktor 1 - (V 2/2), amely szorozva x 2 és t 2.

Mi lehet kizárni ezt a tényezőt, ha írunk a végső átalakulás a koordinátákat és az időt az alábbiak szerint:

Ez a híres Lorentz-transzformáció, elnevezett a holland fizikus Hendrik Lorentz teoretikus, aki 1904-ben vezette a képletű (10.9), és ezáltal az átállás előkészítésére, hogy a relativitáselmélet.

Ez könnyen ellenőrizhető, hogy a szubsztitúció a (10.9) az egyenletben (10.2) a Lorentz-transzformáció, mint amilyennek lennie kellene, ez az egyenlet alakítjuk egy egyenlet a gömb alakú felület (10.1) a rögzített koordináta-rendszerben. Azt is könnyű belátni, hogy ha

V / a -> 0 Lorentz transzformáció megy végbe Galileo transzformáció (9.2).