A szög a vektorok

Amikor arról beszélünk, vektorok, mint irányított vonalszakaszok, olyan fogalmakkal, mint vektor hosszát és szögét a vektorok közötti tűnik természetes és intuitív. Ebben a cikkben, mi határozza meg a szög a síkban és a háromdimenziós térben, így grafikus ábrázolása. Összpontosít módszereket találni a koszinusza a szög (és a szög) vektorok között, részletesen elemezzük a konkrét példákat döntések és feladatok.

Oldalnavigáció.

A szög a vektorok egy síkban az űrben.

Hagyja a gépen, vagy a háromdimenziós térben két nem nulla vektor és készlet. Ellenszegültek tetszőleges pont O vektorok. Aztán ott van a következő meghatározást.

És az a szög a vektorok által bezárt szög a sugarak OA és OB.

A szög a vektorok és fogjuk jelölni.

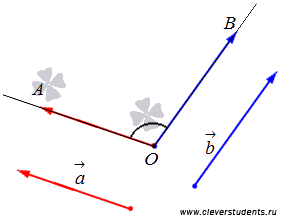
Magától értetődik, hogy a szög a vektorok értékeket vehet fel 0-ról, vagy ami ugyanaz, a hogy.

A vektorok és CO-irányította a vektorok és az ellenkező irányba.

Vektorok nevezzük merőleges. ha a köztük lévő szög van (radián).

Ha legalább egy a vektorok és a nulla, a szög nem meghatározott.

Megtalálása a szög két vektor, példákat és megoldásokat.

A koszinusza közötti szög a vektorokba, és így a szög maga általában megtalálható akár egy skaláris szorzata vektorok segítségével, vagy a tétel a koszinuszok egy háromszög alakult a vektorok és.

Nézzük ezeket az eseteket.

A definíció szerint a skalár szorzat. Ha a vektorok és nem nulla, akkor tudjuk osztani mindkét oldalát ennek az egyenletnek a termék által a hosszúságú vektorok és, megkapjuk a képlet megtalálása koszinusza közötti szög nulla vektorok. . Ez a képlet használható, ha ismeri a hossza a vektorok és skalár termék.

Számítsuk ki a koszinusza közötti szög a vektorokba, és kap a szög is, amennyiben és azonos hosszúságú vektorok 3 és 6, illetve, és azok dot termék egyenlő -9.

A feladatok vannak a szükséges mennyiségben a képlet alkalmazását. Kiszámítjuk a koszinusza közötti szög vektorokat és :.

Most az a szög, vektorok között :.