A vektorok a térben, és példák a általános képletű
Alapfogalmak és meghatározások vektorok
Vektor úgynevezett irányított vonalszakasz, azaz, egy szegmens, amely meghatározott, amely a végei tartják az elején, és mi - vége (1. ábra).
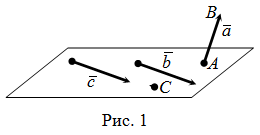
Ha az elején a vektor egybeesik annak végén, egy ilyen vektort nevezzük null és kijelölt. (1. ábra egy nulla vektor).
Megjegyzés. Bármelyik pontján a tér kezelik, mint egy nulla vektor.
Hossza vagy modulusa vektor hossza a szegmens.
Megjegyzés. A hossza a nulla vektor nulla:
Vektor, amelynek hossza megegyezik az egyik, az úgynevezett egység.
Kollineáris és a nem-kollineáris vektorok térben
Két nulla vektort nevezzük egyenesre vagy párhuzamos. ha tartoznak azonos vagy párhuzamos vonalak. (Az 1. ábrán ezek a vektorok).
Lemma. Ha két nem nulla vektor és egy egyenesbe esik, akkor van egy szám, amely az egyenlő:
Co-irányított, és szemben vektorok térben
Két nem nulla vektor és egyenesre nevű codirectional. ha irányok egybeesnek (); és ellenkező - egyébként ().
Vektorok nevezzük egyenlő. ha társrendezője, és hosszuk megegyezik.
Jóváhagyása. Bármely pontjáról tér el lehet halasztani vektor egyenlő ez, és az egyetlen.
Két nem nulla vektorokat nevezik szemben. ha hosszuk egyenlő, és ezek ellentétes irányú.
A vektorokat nevezzük egy síkban vannak. ha halogató ugyanarról a helyről fognak feküdni a síkban.
Megjegyzés. Bármely két kollineáris vektor egy síkban vannak; három vektor, amelyek között van két egyenesre és egy síkban.
Jóváhagyása. Ha a vektor lehet képviselt lineáris kombinációjával vektorok:
A vektorok egy síkban vannak.
Tétel. Bármely olyan vektor, bontható három vektor adja nem egy síkba eső, a tágulási együtthatók meghatározására egyedileg:
Ha a pontok a térben meghatározott és a koordinátákat, majd megtalálni a koordinátákat a koordinátákat kell lennie a végén a pont vektor megfelelő kivonja a kezdőpont koordinátái: