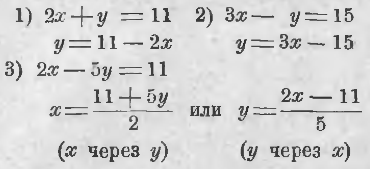Az egyenletek az első fokú, két ismeretlenes Matematika

55. Az egyenlet két ismeretlen. Most tekintsük az egyenlet

Ez a feladat a felvétel: megtalálni a számszerű értékeket az x és y, hogy a binomiális 5x + 3y bizonyult száma egyenlő a 18.

Tudjuk, hogy ha a két távú lenne, ha csak egy ismeretlen számot, és még akkor is tudtuk, hogy megoldja a megfelelő egyenletet. Ezért van egy szempont, hogy az egyik ismeretlen, hogy hogyan lehet felesleges: ha ahelyett, hogy az ismeretlen y, például, hogy néhány szám, akkor a kapott egyenletet egy ismeretlen.

És ha igen, akkor ez az egyenlet kellene rengeteg megoldás, és kiderül, előállítási módjuk, adjunk egy az ismeretlenek, például, y és tetszőleges értékeket, ha nyert 1. egyenlet meghatározzuk az ismeretlen lesz egy ismeretlen x. Ahhoz, hogy ez a munka több sorrendben, majd az eredmények rekord a táblázatban.

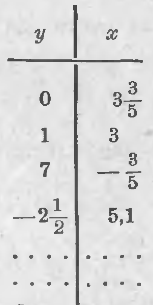
Mi most hogy y értéke 0, t. E., feltesszük, hogy az y = 0 (írva az első sorban a táblázatban). Akkor mi egyenlet foglalkozni

(Táblázat rekord ez a szám, a második oszlopban című betűk x).

Tehát van egy egyenlet megoldása: y = 0, és x = 3 (3/5) (ha ezeket az értékeket behelyettesítjük a binomiális helyett x és y, az a követelmény, hogy a binomiális száma egyenlő a 18, indokolt:
3 * 3 (3/5) + 3 * 0 = 18).

Adunk egy y értéke 1, azaz, azt feltételezzük, hogy az y = 1 (második sor a táblázatban) ..; akkor megkapjuk

5x = 18 - 3, vagy 5x = 15, és X = 3 (rögzített a 2. vonal). Tehát azt találtuk, a második egyenlet megoldása y = 1 és x = 3.

Most, hogy y érték 7, azaz feltesszük, hogy y = 7 ..; akkor megkapjuk az egyenlet 5x + 21 = 18, ahol 5x = -3 és x = -3/5 (lásd. a harmadik sorban a táblázatban).

Tegyük fel, még y = -2½; Ezután 5x + 3 (-2½) = 18, illetve 5x - 7½ = 18, ahol 5x = 25½ és x = 5 (1/10) = 5,1 (lásd 4. sor a táblázat.). Ez a munka lehet hosszabbítani, amennyiben szükséges. Szóval, az egyik egyenlet két ismeretlen végtelen sok megoldás; megszerezni azokat meg kell adni egy ismeretlen, és tetszőleges értéket a kapott egyenletrendszer meghatározza minden egyes alkalommal egy másik ismeretlen.

. Figyelembe véve az előző táblázat, emlékeztetve ítélet 49., azt kell megállapítani: mi voltunk a független változók y, x - függő, vagy függvénye x y - a.

Mi lehet kissé felgyorsítja a munkát, hogy megoldást találjon az egyenletben. Számozott y egy bizonyos számú (még, elvégre y minden alkalommal cserélni egy ismert szám); majd az egyenlet 5x + 3y = 18, láthatjuk, hogy az egyenlet egy ismeretlen x, és megoldani ezt az egyenletet:

5x = 18 - 3Y; X = (18 - 3y) / 5

Mi lehet szavakkal kifejezni ezt az eredményt, mert már azonosított ebben az egyenletben y keresztül x.

Most, az alábbi képlet szerint (18 - 3y) / 5, könnyen találhatunk számos megoldás, ami számítások szem előtt tartva. Tegyük fel, például, y = 2, akkor szükséges, hogy (3) szorozva (2), megkapjuk -6; szeres (18) és (-6) - kap 12 és osztva 5 - kapjuk az x = +2 (2/5). Több hagyja y = 10; majd (-3) + (+10) = -30; (+18) + (-30) = -12; (-12). (+5) = -2 (2/5), t. E. X = -2 (2/5) és a t. D.

Vegyük a következő egyenletet:

Vesszük a független változó x, míg a függőség y és y által meghatározott x. Ezt meg lehet tenni két módszerrel:

Lehet kényelmesebb a második fogadását az 1., miután annak végrehajtását könnyebb képzelet, ha az a kívánatos, hogy elvégzik a y-x és az elme.

Most találunk tetszőleges számú egyenlet megoldásai: 1) X = 0; y = -5 (2/3); 2) x = 1; y = -4; 3) x = 1; y = -7 (1/3) és a t. d.

Meg kell hozzászoktatni gyorsan (a fejemben) határozza meg az egyik ismeretlen az egyenlet két ismeretlent egy másik. példák:
f55_3