Beírt és körülírt körök

Existence :. Rajzolj egy kört középpontú $ O $ sugarú $ OK \ $ Mivel a pont $ O $ van három bisectors, ez egyenlő távolságra az oldalán a háromszög az ABC $ $. Ez $ OM = OK = OL $. Ezért a szerkesztett kör is áthalad a ponton $ M \ és \ L $. Mivel $ OM, OK \ és \ OL $ - merőlegesek az oldalán a háromszög, akkor a tétel a kör érintője épített érintő mindhárom oldalán a háromszög. Következésképpen alapján az önkényesség a háromszög, a háromszög bármelyik kör írható,.

Egyediség: Tegyük fel, hogy a háromszög $ ABC $, megadhat egy másik kör közepén $ O „$. A központ egyenlő távolságra egy háromszög oldalai, és így egybeesik a ponton $ O $ és sugara hosszával megegyező $ OK $. De akkor ez a kör, amely egybeesik az első.

Következmény 1: A központ a beírható kör a háromszög metszéspontjában annak bisectors.

Íme néhány tény fogalmához kapcsolódó a beírt kör:

Nem minden négyszög lehet beírt kör.

Mindenesetre érintőnégyszög összegével szemben lévő oldala egyenlő.

Ha az összeg a két oldalán egy konvex négyszög egyenlő, akkor a kör írható, benne.

A körülírt kör

Ha az összes fekszenek a kerülete egy sokszög vertex, akkor a köré írt kör az úgynevezett poligon (3.).

Egyediség: Tegyük fel, hogy néhány háromszög $ ABC $ lehet leírni egy kör közepén $ O „$. Her egyenlő távolságra a központtól, a háromszög csúcsait, és így egybeesik a ponton $ O $ és sugara hosszával megegyező $ OC. $ De akkor ezt a kört egybeesik az első.

Következmény 1: Center köré írt kör háromszög egybeesik a metszéspontját a midperpendiculars.

Íme néhány kapcsolatos tényeket a koncepció a körülírt kör:

A négyszög nem mindig lehet leírni egy kört.

Mindenesetre húrnégyszögben összege szemközti szögek egyenlő $ ^ 0 $.

Ha az összeg a szemközti szögek egy négyszög $ ^ 0 $, akkor körül lehet leírni egy kört.

Példa problémát a koncepció a körülírt kör és a beírt

Az egyenlő szárú háromszög alapja 8 cm, az oldalsó oldalon egyenlő 5 cm. Megtalálni a sugara a beírt kör.

Tekintsük a háromszög $ ABC $. By Következmény 1, tudjuk, hogy a központ a beírt kör metszéspontjában a szögfelező. Bisectors $ AK $ és $ BM $, ami metszi a ponton $ O $. Döntetlen a merőleges OH $ $ azon a ponton $ O $ oldalán $ BC $. Rajz ábrázol:

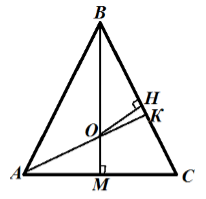
Mivel a háromszög egyenlő szárú, akkor a BM $ $, valamint a középső és a magasság. Pitagorasz $ ^ 2 ^ 2 ^ 2, \ BM = \ sqrt ^ 2- \ frac ^ 2 >> = \ sqrt = \ sqrt = 3 $. $ OM = OH = R $ - a kívánt sugara a beírt kör. Mivel az MC $ $ $, és $ CH szegmensek metsző érintők, akkor a tétel a metsző érintők van $ CH = MC = 4 \ $ cm. Következésképpen $ BH = 5-4 = 1 \ $ cm. $ BO = 3-R $. A háromszög $ $ OHB, a Pitagorasz-tétel, megkapjuk: