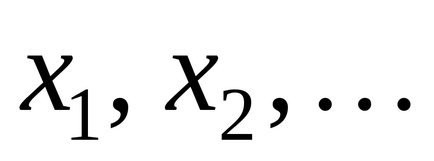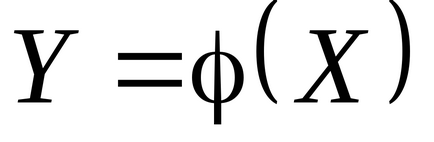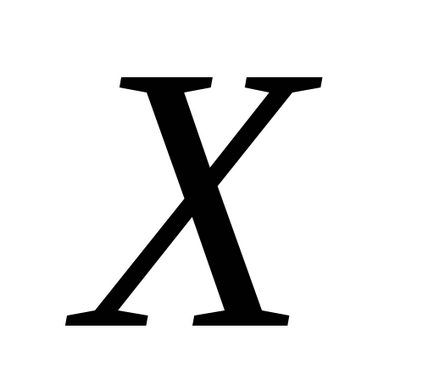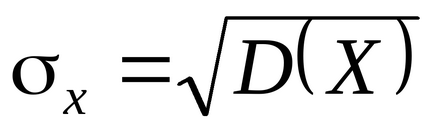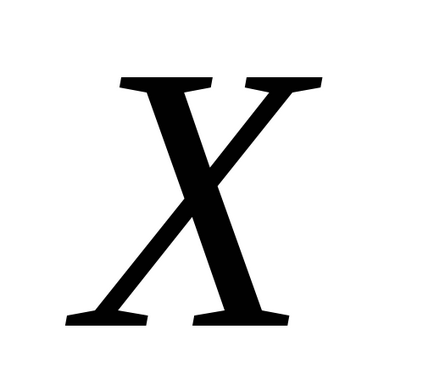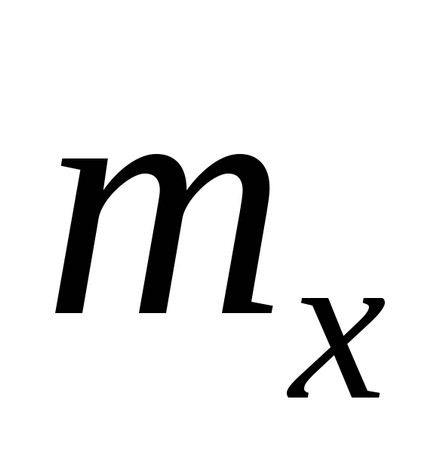Előadás №05 (4 távú)

A számszerű jellemzőit valószínűségi változók következők: elvárás, szórás, momentumok különböző megrendelések, stb

enged

- diszkrét valószínűségi változók figyelembe értékekvalószínűségekkelvolt.

Elvárás (st), vagy az átlagos érték dm

az a szám

Feltételezve, hogy a sorozat konvergál teljesen.

Ha ez a szám

eltér, akkor azt mondjuk, hogy az SVEz véges st

ha

- folytonos valószínűségi változók A valószínűség-sűrűség, akkor st által meghatározott szerves

feltéve, hogy konvergál teljesen.

enged

- diszkrét valószínűségi változók forgalmazásával törvény (2.1) (Tárgy: skalár valószínűségi változók) és- funkciója a rv Ezután a törvény eloszlása ​​véletlen változókEz a forma táblázat. 7.1 (Tárgy: skaláris valószínűségi változók). Szerint (1.1) egyenlet st véletlen változóképlet határozza meg

.

Ha azonban

- folytonos valószínűségi változók A valószínűség-sűrűség, hogy általánossá az előző érvek, megkapjuk a képlet a MO véletlen változóformájában

Példa 1.1. A készpénz tombola 200 kiadott jegyek. Játszott a nyereség összegének 50 rubel. két - 25 rubel. Tíz - 1 dörzsölje. Keresse az átlagos nyereség értéke, ha vásárolt egy jegyet.

Példa szerint, a D 2.1 (Tárgy: skaláris véletlen értékek) elosztó jog d.s.

- win - ez (2.2) (Tárgy: A skalár valószínűségi változók).

A képlet szerint (1.1), az átlagos értéke a győztes

Így az átlagos nyereség a lottón egyenlő 55 kopecks. ▲

1.2 példa. a sűrűségfüggvény véletlen változók

úgy néz ki,

A képlet szerint D (1,3)

. ▲

Hadd magyarázzuk alaptulajdonságait az elvárás.

1 0. MO az előfordulások számát események

Az egyik tesztben azonos valószínűséggelezt az eseményt.

2 0. MO állandó értéket nem véletlenszerű

jelentése.

3 0. Constant szorzó, nem véletlenszerű

Meg lehet venni, mint egy jel a várakozás.

4 0. Minden véletlen változók (függő vagy független) st összeg SV

ésösszegével egyenlő MO ezeket az értékeket:

5 0. független valószínűségi változók st művek SV

ésegyenlő a termék a st SV azaz

1.3 példa. Keresse MO összege a pontok számát, hogy kieshet, ha dobott két kockával.

Legyen D

és- száma csökkent pontot az első és a második csontok, ill. Diszkrét valószínűségi változókésveszi a értéke 1, 2, 3, 4, 5 és 6 azonos valószínűséggel. Ezután a (1.4) és (1.1) szükséges MO

. ▲

MO Ez jellemzi a középérték dm SV eltérése

annak matematikai elvárás (átlag) .. Gyakran nevezik a SV értéknazyvaetsyatsentrirovannoy SV

Diszperzió vagy szórás

véletlen változóEz egy matematikai elvárás a négyzetes eltérés a véletlen változóannak matematikai elvárás:

A négyzetgyöke variancia nevezzük mean-square (kvadratikus) eltérés d.s.

és jelöljük, azért, hogy.

Diszkrét valószínűségi változók

, figyelembe értékekvalószínűség,, diszperziót alábbi egyenlettel határozható meg

Folyamatos véletlen változók

diszperziót alábbi egyenlettel határozható meg

ha ez az integrál létezik. itt

- sűrűségfüggvénye dm.

A tulajdonságait a MM és meghatározzuk a diszperziós van

.

Tehát, diszkrét valószínűségi változók

Folyamatos véletlen változók

(2.4) a formája

Képletek (2.4) és (2.5) sokkal kényelmesebb, hogy kiszámítja a diszperzió.

Megjegyzés. A meghatározása diszperziót (2,1) d.s.

Ebből következik, hogy. Ha a szórás kicsi, akkor minden idejét az összeg (2.2) is kicsi. Ezért az érték, aholnagy, kell egy kis valószínűségű. Más szóval, a kis szórás nagy eltérések d.s.tőle MOvalószínű. egyenlőségazt jelenti, hogyazok értékei, valószínűségegyenlő nullával. Más szóval,azt jelenti, hogyvalószínűséggel egységét.

Példa 2.1. Keresse meg a szórás a rv

, adott valószínűség-eloszlási törvény