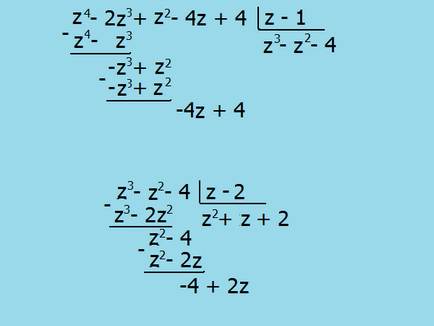Hogyan készítsünk egy sor gyökér

Használja a gyökér meghatározása. mint egy matematikai művelet, amelyből az következik, hogy a gyökér kivonat - az inverz művelet az építési teljesítmény. Ez azt jelenti, hogy a szám lehet kivenni a gyökér, feltéve csökkenése radicand számának megfelel alkalommal hatványozást hozott egy számot. Például, hogy tanuljanak egy négyzet kornyachislo 10, meg kell osztani a többi kifejezés a négyzetgyök alatti tíz négyzeten.

Pick radicand egy ilyen tényező, kivetése, amely alatt a gyökér valóban egyszerűsíteni a kifejezést - különben a művelet lesz értelme. Például, ha van száma 128, akkor a megjelölés alatt lehet venni, például, 5-ös szám, hogy három (köbgyökét) alatt a radikális jele az index, a szám a négyzetgyöke 128 kell majd osztva 5 a kocka: ³√128 = 5∗³√ (128 / 5³) = 5∗³√ (128/125) = 5∗³√1.024. Ha a jelenléte egy törtszám alatt gyökös megjelölés nem mond ellent a feltételeket, a probléma, az oldatot lehet hagyni, mint olyan. Ha szükséges egyszerűbb kiviteli alaknál, az első szünet radicand mint egész szám szorzók, a kocka egyik gyökérben, amely az m egész szám például :. ³√128 = ³√ (64∗2) = ³√ (4³∗2) = 4∗³√2.

Használja a kiválasztási szempontok radicand számológép, ha kiszámítjuk a mértékét az elme nem lehetséges. Ez különösen igaz, hogy a gyökerek a kitevő nagyobb, mint kettő. Ha rendelkezik internet-hozzáféréssel, akkor számítások elvégzésére beépített keresők a Google és Nigma számológépek. Például, ha meg kell találni a legnagyobb egész szorzó, amely lehet kivenni jegyében köbgyök számának 250, menjen a Google, írja be a keresett „6 ^ 3”, hogy ellenőrizze, hogy a render a megjelölés nem lehet a gyökere hat. Finder megmutatja olvasatából 216. Sajnos, a 250 nem osztható maradék nélkül az adott számot. Ezután adja meg a keresési 5 ^ 3. Az eredmény az lesz a 125, és ez lehetővé teszi, hogy megtörje a 250 szorzók 125 és 2, és így elvenni a megjelölést kornyachislo 5, maga mögött hagyva a 2-es szám.

Amikor eltávolítja a gyökerek kényelmesen használható speciális táblázatok vagy táblázatok logaritmikus gyökerek - hogy jelentősen csökkenti az idő, hogy megtalálják a megfelelő megoldásokat.

• mark vonás

Algebrai kifejezések van szükség számos területen a matematika, beleértve a döntés az egyenletek magasabb fok, differenciálódás és integráció. Ez többféle módszer, köztük faktoring. Ahhoz, hogy ezt a módszert, meg kell találni, és egy közös tényezőt ki a zárójelben.

A bevezetése közös tényező ki a zárójelben - az egyik leggyakoribb módja a faktoring. Ezt a technikát használják, hogy egyszerűsítse a szerkezet hosszú algebrai kifejezések, azaz polinomok. Közös tényező lehet egy szám, egy egytagú vagy kéttagú, és keresni alkalmazza a szorzás disztributív tulajdonság.

Chislo.Posmotrite óvatos az együtthatók mindegyik eleme egy polinom, tudjuk osztani őket ugyanazt a számot. 4 lesz • (3 • z³ + 4 • ZZ - 1) 4 nyilvánvaló tényező 4. Az átalakítás után - például az expressziós 12 • z³ + 16 • ZZ. Más szóval, ez a szám a legkisebb közös egész osztója minden együttható.

Odnochlen.Opredelite tartalmazzák-e ugyanazon változó az egyes kifejezéseket a polinom. Tegyük fel, hogy ez így van, most nézd meg a tényezőket, mint az előző esetben. 9. példa • z ^ 4 - 6 • z³ + 15 • ZZ - 3 • Z.

Minden egyes eleme a polinom tartalmaz egy variábilis z. Továbbá, minden együttható - többszörösei 3. Következésképpen, egy közös faktornak egytagú 3 • z: 3 • z • (3 • z³ - 2 • ZZ + 5 • Z - 1).

Dvuchlen.Za zárójelben kiszabott közös tényezője a két elem, és egy változó szám, amely egy olyan megoldás közös polinom. Ezért, ha -dvuchlen tényező nem egyértelmű, meg kell találni legalább egy gyökér. Kiemelés szabad kifejezés a polinom együtthatót nélkül változtatható. Most kell alkalmazni a helyettesítési módszer egy általános kifejezés az összes szerves osztója a konstans tag.

Vegyünk egy példát: z ^ 4 - 2 • z³ + ZZ - 4 • Z + 4. Ezután ellenőrizze, hogy bármely egész szám osztója 4 gyökere az egyenlet z ^ 4 - 2 • z³ + ZZ - 4 • Z + 4 = 0. egyszerű helyettesítés lokalizálják z1 = z2 = 1, és 2, ez azt jelenti, hogy a zárójelben lehet venni binomials (Z1) és (z2). Ahhoz, hogy megtalálja a többi kifejezés, a soros hosszú részlege.