Hogyan lehet megtalálni a szöget a két vektor közötti

Vektor - egy szegmens egy adott irányba. A szög a vektorok egy fizikai érték, mint például, amikor a vektor hossza a vetülete a tengelyen.

A szög a két nem nulla vektorokat úgy határozzuk meg, hogy kiszámítjuk egy skaláris szorzata. A skalár-szorzat definíciójából a termék hosszának a vektorokat koszinusza a köztük lévő szög. Másrészt, a skaláris szorzata két vektor egy koordinátáit (x1, y1), és b koordináták (x2; y2) kiszámítása a következő képlet: AB = x1x2 + y1y2. E két módszer a megállapítás a skalár szorzat könnyű megtalálni a szöget a vektorok.

Keresse meg a hossza a vektor vagy modulokat. A mi a és b vektorok: | a | = (X1² + y1²) ^ 1/2, | b | = (X2² + y2²) ^ 1/2.

Find skalár szorzata vektorok, megszorozzuk helyzetük párban: AB = x1x2 + y1y2. A skalár-szorzat definíciójából ab = | a | * | b | * cos # 945;, ahol # 945; - közötti szög a vektorok. Akkor azt találjuk, hogy x1x2 + y1y2 = | a | * | b | * cos # 945;. Ekkor cos # 945; = (X1x2 + y1y2) / (| a | * | b |) = (x1x2 + y1y2) / ((x1² + y1²) (x2² + y2²)) ^ 1/2.

az a szög, # 945; alkalmazásával Bradis táblázatokat.

Abban az esetben, háromdimenziós térben adunk a harmadik koordináta. A vektorok egy (x1; Y1; Z1) és b (x2; Y2; Z2) általános képletű a koszinusza a szög ábrán látható.

Skaláris termék - egy skalár jellemző hosszúságú a vektorok és a köztük lévő szög.

A repülőgép - az egyik alapvető fogalmak a geometriában. Sík felületre, amelyre az állítás igaz - bármely összekötő vonal két pont annak kizárólagos tulajdonában felületen. Plane lehet kijelölni a görög betűk α, β, γ, stb Két sík mindig metszik egy egyenes vonal, amelyik mindkét sík.

Tekintsük a félsíkra α és β által alkotott két síkja egymást metszi. A szögben, amelyet egy egyenes vonal, és a két fél-sík, alfa, és β nevezzük diéderes szöget. Ebben a fél-síkot egy diéder nevezett metszettel, egy vonal metszi a sík a diéderes szöget nevezzük egy él.

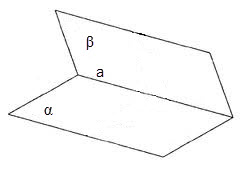
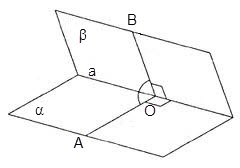
A diéderes szöge, mint a gép szög, fokokban mérve. Ahhoz, hogy mérjük a diéderes szög szükséges annak arcok, hogy válasszon egy tetszőleges pont O. mindkét síkban keresztül O végzik két gerenda merőleges a szélén egy. A képződött szög AOB úgynevezett lineáris szög diéder egy szélén egy.

Így, mérjük a szög két egymást metsző síkban α és P a szöget kell mérni a lineáris ∠AOB.

Vector geometria nevezzük irányított vonal szegmens vagy egy rendezett pár pontok euklideszi térben. A hossza a vektor - egy skalár egyenlő a négyzetgyöke számtani négyzetének összege a koordináták (komponens) a vektor.

• Alapvető ismeretek a geometria és algebra.

A koszinusza közötti szög vektorok között találjuk a skaláris szorzata. Összege termékek a megfelelő komponenseket a vektor egyenlő a hosszuk a koszinusz az a köztük lévő szög. Legyen a két vektor: egy (x1, y1) és b (x2, y2). Ezután a skaláris szorzata felírható formájában az egyenlőség: x1 * x2 + y1 * y2 = | a | * | b | * cos (U), ahol U - közötti szög a vektorok.

Például, a koordinátáit a vektor egy (0, 3), és a B vektor (3, 4).

Expresszáló kapott egyenletből cos (U) kapunk, hogy a cos (U) = (X1 * x2 + Y1 * Y2) / (| a | * | b |). A példában a képlet után helyettesítési ismert koordináták formájában: cos (U) = (0 * 3 + 3 * 4) / (| a | * | b |) vagy COS (U) = 12 / (| a | * | b | ).

A hossza a vektor a képletek: | a | = (X1 ^ 2 + Y1 ^ 2) ^ 1/2, | b | = (X2 ^ 2 + y2 ^ 2) ^ 1/2. Behelyettesítve a koordinátáit a vektorok egy (0, 3), b (3, 4) kapunk, rendre, | a | = 3, | b | = 5.

Behelyettesítve ezeket az értékeket a képlet cos (U) = (x1 * x2 + y2 y1 *) / (| a | * | b |), hogy a választ. A detektált hossza vektorok kap, hogy a koszinusz közötti szög a (0, 3), b (3, 4) egyenlő: cos (U) = 12/15.

Ha minden megfelelően tudja számolni, a koszinusza a szög kisebbnek kell lennie, mint egy. Mivel hosszúságú vektor nem lehet negatív.

Ha a hossza az egyik vektorok egyenlő nullával, akkor ez egy nulla vektor, majd közötti szög a vektor és a másik 90 fokos.

Vektor - az irányított vonalszakasz, amelynek egy bizonyos hosszúságú. A hely, ez határozza meg a három előrejelzések a megfelelő tengelyek. Lehetőség van az a szög, a vektor és a gépet. ha azt képviseli a koordinátákat a normál, azaz általános egyenlete.

Plane - ez a fő alakja, térbeli geometria, amely részt vesz az építési kétdimenziós és háromdimenziós alakzatok, például háromszög nik, négyzet, téglalap, prizma, kör, ellipszis, stb Minden esetben arra korlátozódik, hogy bizonyos meghatározott vonalak metszik egy zárt alakzatot.

Általában egy repülőgép nem korlátozza semmi, kiterjed mindkét oldalán a képet közvetlenül. Ez a végtelen lapos alakú, amely azonban lehet a következő egyenlet adja, azaz a véges számok, amelyek koordinátái a normál vektor.

A fentiek alapján, lehetőség van a szög a vektor és minden síkon. a következő képlet segítségével a koszinusz a szög két vektor. Rendező szegmensek lehet elhelyezni a térben a kívánt, azonban mindegyik vektornak olyan tulajdonsága, hogy lehet mozgatni elvesztése nélkül lényegi jellemzőitől, irányát és hosszát. És ez szükséges használni kiszámításához közötti szög vektorok egymástól helyezi őket vizuális kiindulópontja.

Így, tegyük fel, hogy adott egy vektorban V = (a, b, c), és a sík • x + B • y + C • z = 0, ahol A, B és C - a koordinátákat a normál N. Ezután a koszinusza a szög α vektorok között V és N egyenlő: cos α = (a • a + b • b + a • C) / (√ (a² + b² + s²) • √ (a² + V² + C²)).

Kiszámításához fokban vagy radiánban, meg kell kiszámítani a kapott kifejezés az inverz koszinusz, azaz arkusz: α = arssos ((a • A + B • B + a • C) / (√ (a² + b² + s²) • √ (a² + V² + C²))).

Példa: kap közötti szög a vektor (5, 3, 8) és a sík. adott általános egyenlete 2 • x - 5 • y + 3 • z = 0.Reshenie: kisülés normál vektor a sík koordináták N = (2, -5, 3). Helyettesítse az összes ismert értékeket a fenti képlet: cos α = (10 + 15 + 24) / √3724 ≈ 0,8 → α = 36,87 °.

Mérési értékek sík szöge fokban találták az ősi Babilonban hosszú a keresztény kor előtt. Lakói az állapotban inkább hatvanas számrendszer, így az osztály szögek 180 vagy 360 egység most úgy néz ki, egy kicsit furcsa. Azonban tartózkodik a modern rendszer SI-egységek, amelyek többszörösei pi, nem kevésbé furcsa. Ez a két lehetőség nem kizárólagosan szögek használt megnevezések ma, így a feladat fordítására értéküket gradusnuju intézkedés előfordul elég gyakran.

Ha gradusnuju intézkedés szükséges lefordítani a szöget radiánban feltételezzük, hogy egy fokkal számának felel meg a radiánban egyenlő 1/180 frakció Pi. Ez a matematikai állandó végtelen tizedes helyek számát, így a konverziós tényező radiánban fok is egy végtelen tizedes tört. Ez azt jelenti, hogy teljesen pontos értéket decimális formátumban nem kap ki, így a konverziós tényező kell kerekíteni. Például, pontossággal egy milliárdod a számított arány egyenlő egység 0,017453293. Miután kerekítés a szükséges számú számjeggyel, oszd el ezt a tényezőt az eredeti szám a radiánban, és kapsz egy intézkedés fokos szögben.

Megoldásában matematikai problémák szakaszok kapcsolatos geometria, gyakori képlet, amelyben a szögek vannak kifejezve nem radiánmérték és részvények Pi. Ha kap egy oldatot tartalmazó ez az állandó, átalakítani, hogy a fok helyére π szám 180. Például, ha a központi szög által meghatározott expressziós π / 4, ez azt jelenti, hogy egy intézkedés annak mértéke 180 ° / 4 = 45 °.

Corners ki lehet fejezni és egységek, amelyek az úgynevezett „forradalom”. Ez az egység felel meg 360 °, így a problémák konverzióval merülnek fel problémák. Például, ha a szög beállítási állapotok egy fél fordulattal, ez megfelel 1,5 * 360 = 540 ° ívben mérések.

Néha az egyenes szög említett geometriai problémákat. Ez alkotja két gerenda ellentétes irányban, azaz, fekvő egy egyenes vonal. A szám 180 expressziójához értékének egyenes szög fokokban.

A Földmérési, csillagászat fok vannak osztva kisebb egységekre, amelyek a saját nevét - perc és másodperc. Ez az osztály gyökerei ugyanazon a helyen, és fok, így minden egyes fokozat magában foglalja a 60 perc, vagy 3600 másodperc. Ezekkel a számokkal, amikor a másodpercek és percek kell helyettesíteni tizedfokban. Például, szög 11 ° 14'22 „megfelel a tizedes tört közelítőleg egyenlő 11 + 14/60 + 22/3600 ≈ 11,2394 °.

Vektor a sokdimenziós tér által meghatározott koordinátáit kezdőpont és a meghatározó pontok annak nagyságát és irányát. A különbség a két irány vektorok határoztuk szög értékének. Gyakran mindenféle problémákat fizika és a matematika felkérik, hogy megtalálja önmagát nem a szöget, és a származtatott érték azt a trigonometrikus függvények - sine.

Meghatározására használhatja sinusaugla két vektor ismert képlet skalár szorzás vektorok. Az ilyen formulák formájában léteznek két, legalább. Az egyik közülük, mint egy változó részt koszinusza a kívánt szöget. tudva, hogy lesz képes kiszámítani a szinusz.

Tedd egyenlőség és elszigetelni a koszinusz. Képlet szerint a skalár szorzata vektorok egyenlő hosszuk, megszorozzuk egymással és a koszinusza a szög. és a másik - az értékek összege a koordináták mindegyik tengely mentén. Egyenlővé mindkét képletben a következtetés vonható le, hogy a cosinus a szög legyen egyenlő összeget termékek koordinátákat a termékhez viszonyítva a hossza a vektorok.

Feljegyezzük a kapott egyenletet. Ehhez meg kell határozni azokat a koordinátákat a két vektor. Tegyük fel, hogy azok egy háromdimenziós koordináta-rendszerbe, és a kiinduló ponttól költözött a tetején a rács. Iránya és mértéke az első vektor kap pontot (Xj, Y |, Zi), egy második - (X₂, Y₂, Z₂), és az a szög címke levél γ. Ezután a hossza az egyes vektorok lehet kiszámítani, például úgy, hogy a Pitagorasz tétel által alkotott háromszög kivetítjük az egyes koordinátatengelyeken: √ (X₁² + Y₁² + Z₁²) és √ (X₂² + Y₂² + Z₂²). Helyettesítsük ezeket a kifejezéseket a képlet megfogalmazott az előző lépésben, és akkor kap a egyenletet: cos (γ) = (Xj * X₂ + Yj * Y₂ + Zj * Z₂) / (√ (X₁² + Y₁² + Z₁²) * √ (X₂² + Y₂² + Z₂²)).

Használja a tény, hogy a négyzetösszege értékeit szinusz és koszinusz a szög azonos nagyságrendű mindig ad egy. Tehát felemelte amelyet az előző lépésben a kifejezés a koszinusznégyzetes és levonják a készüléket, majd keresse meg a négyzetgyök, úgy dönt, a problémát. Feljegyezzük a kívánt képletet egy általános formája: sin (γ) = √ (1-cos (γ) ²) = √ (1 - ((Xj * X₂ + Yj * Y₂ + Zj * Z₂) / (√ (X₁² + Y₁² + Z₁² ) * √ (X₂² + Y₂² + Z₂²)) ²) = √ (1 - ((Xj * X₂ + Yj * Y₂ + Zj * Z₂) ² / ((X₁² + Y₁² + Z₁²) * (X₂² + Y₂² + Z₂²) )).

Műveletek vektorokkal gyakran okoz nehézséget a tanulók. Annak ellenére, hogy a rendelkezésre álló korlátozott számú formulák, amelyekkel kezelhető, bizonyos feladatokat okozhat komplexitás és a megoldás. Különösen nem az összes középiskolás diákok tudják számítani a szög a vektorok.

Megjegyezzük, hogy a számítás a szög közötti bármely két vektor csökken megtalálása vektorok között. amelynek egy közös pont. Ez gyakran okoz félreértést, de magyarázható egyszerűen. Ahhoz, hogy két, azonos síkban vektorok indul egy ponton, akkor kell végrehajtani egy műveletet a párhuzamos közlekedés. De ez az eljárás nem érinti a kívánt értéket.

Megjegyzés általános meghatározása a szög két vektor. ez segít meghatározni egy ötlet, hogy mi szükséges a feladat. Mivel a szög - ez nem teljesen, hanem egy bizonyos valóság jelöli a legrövidebb összeg, amellyel a forgatáshoz egy vektorba (tekintettel a kiindulási pont), a codirectional a második. Fontos szem előtt tartani, hogy a kívánt szög értékének kell lennie a tartományban nulla 3,14 radián.

Ne felejtsük el, hogy ha foglalkozunk egyenesre vagy párhuzamos vektorok. szög értéke nulla fok esetén a CO-irányított és 180 - többirányú vektorok. Ebből következik a definícióból, mert meg kell forgatni a második vektort hogy változtassa meg irányát.

Használd az egyszerű képlet, amely lehetővé teszi, hogy gyorsan kiszámítja a koszinusz szög értéke vektorok között. Ehhez meg kell tudni, hogy a koordinátákat. Koszinusz a szög egy frakciót, amelyben a számláló a skaláris szorzata vektorok, és a nevező - a termék a saját modulok. Ahhoz, hogy megtalálja az első érték a vektorok koordinátái a1, a2, a3 és c1, c2, c3, megtalálják a szorzatösszegében A1C1, a2s2, a3s3. Modulus egyes vektorok a gyökere a második erő a négyzetének összege a koordinátákat.

Lásd, hogy segítse az elektronikus számológépek, amely megadja a paramétereket vektorok kiszámítja a kívánt szögben.