Lineáris függvénye annak tulajdonságait és a menetrend

ahol k és b valós számok.

Tulajdonságok lineáris függvény

Lineáris függvény a következő tulajdonságokkal rendelkezik:

1. y = kx + b - talán még, vagy páratlan funkció;
2. a domain a funkció y = kx + b - egész szám sorban;
3. Az értékrend lineáris függvény - az egész számegyenesen;
4. Ha k nagyobb, mint 0, a funkció növeli, és ha k értéke kisebb, mint 0, akkor a lineáris függvény csökken.

A lejtőn a lineáris függvény

Tényező K a képlet a lineáris függvény a meredekség.

A meredekség határozza meg a szög között a grafikon egy lineáris függvény, és a pozitív irány az X-tengelyen.

A grafikon a lineáris függvény

A grafikon egy lineáris függvény egy egyenes vonal. Itt látható y = 2x + 1 lineáris függvény grafikon

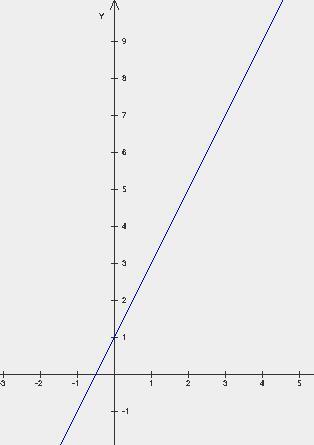
Itt a lejtőn nagyobb, mint nulla, a szög az egyenes y = 2x + 1 X-tengellyel pozitív irányba - akut.

Most pedig lássuk, hogyan kell változtatni a menetrend a lineáris függvény y = 2x + 1, ha a lejtőn tett negatív, azaz a y = -2x + 1

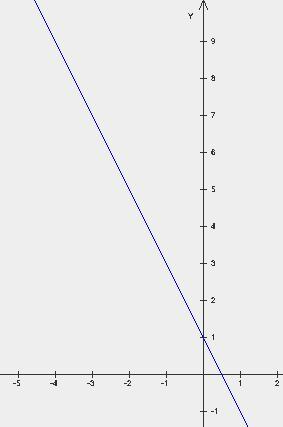
Itt az a szög egyenes y = -2x + 1, pozitív iránya X tengely - tompaszög.

Mint egy lineáris függvény grafikon változik attól függően, hogy a száma b a képlet a lineáris függvény az y = kx + b? Ha b növekedése, a grafikon felfelé eltolt, ha a szám b csökkenése, a grafikon y = kx + b lefelé mozog.

A grafikon a lineáris függvény y = kx + b, akkor lehet építeni magad most a segítségével építő menetrendek. Válassza azt a formáját a funkció „Line: y = k * x + b” és kattintson a „telek”. Végezzünk kísérleteket: set szögletes aránya nagyobb, és kisebb, mint nulla, módosítsa az értékeket a b és látom, hogy a grafikon fog változni a lineáris függvény.