Négyszög derékszög - ez

Az egyik legérdekesebb téma a geometria a tanév - a „négyszög” (Grade 8). Milyen számok léteznek, milyen különleges tulajdonságokkal rendelkeznek? Mi különbözteti meg a négyszögek szögekkel kilencven fokkal? Nézzük meg mindezt.

Milyen geometriai alakzat úgynevezett négyszög

Sokszögek, hogy áll négy oldala, illetve a négy csúcsot (sarkok) nevezik az euklideszi geometria négyszög.

Érdekelt a történelem, az ilyen típusú név számok. A „négy sarka” (ugyanúgy, mint a „háromszög” - három szög „ötszög” - öt szögek, stb ...) A magyar főnév „négyszög” származik.

Azonban a latin (lépett közvetítésével számos geometriai értelemben a legtöbb világnyelven) azt nevezzük négyszög. Ez a szó egy szám Quadri (négy) és egy főnév latus (oldalsó). Így elmondható, hogy az ősi sokszög volt ismert, csak „négyszög”.

By the way, a név (a hangsúlyt a jelenléte a számok ezt a fajta négy oldalán, nem a sarkokban) megtartott néhány modern nyelven. Például az angol - négyszög alakú, és a francia - quadrilatèújra.

A legtöbb szláv nyelvben ez a faj azonosítható számadatok még mindig a szögletek száma, nem az oldalán. Például szlovák (štvoruholníA k), bolgár (chetiriglnik ") Fehéroroszország (" chatyrohkutnіk ") ukrán (" chotirikutnik „), cseh (čtyřúHeLNík), de a lengyel négyszög felhívta a pártok száma - czworoboczny.

Milyen típusú quad tanulmányozzák az iskolai tantervben

A modern geometria 4 féle poligonok négy oldala van.

Azonban, mivel nagyon összetett tulajdonságai közül néhány az iskolai geometria osztályok csak ismerős kétféle.

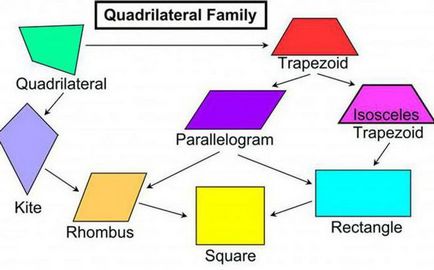
• Paralelogramma (paralelogramma). A szemben lévő oldalain a négyszög egymással párhuzamosan és a, illetve egyenlő párban.
• Trapezoid (trapéz vagy trapéz). Ez a négyszög két szemközti oldalán egymással párhuzamosan. Azonban a másik két fél nem rendelkezik ilyen funkcióval.

Nem vizsgálták az iskolában során geometriai típusú négyszögek

Ezeken van kétféle négyszögek, amellyel a diákok nem ismerik a geometria órák, mert különleges összetettségét.

• Deltoid (kite) - ábra, ahol mindegyik két pár szomszédos oldala egyenlő hosszúságú egymással. A neve ennek a négyszög volt annak a ténynek köszönhető, hogy a megjelenés ő egészen emlékeztet a levél a görög ábécé - „delta”.
• Paralelogramma (antiparallelogram) - ez a szám összetett, mint a neve. Ebben a két ellentétes oldalán egyenlő, de ezek nem párhuzamosak egymással. Emellett a hosszú ellentétes oldalán négyszög metszik folytatásaként másik két rövidebb oldalán.

típusú paralelogramma

Miután foglalkozott a főbb quadok, meg kell figyelni, hogy az alfaj. Szóval, minden paralelogramma, viszont szintén négy csoportra osztjuk.

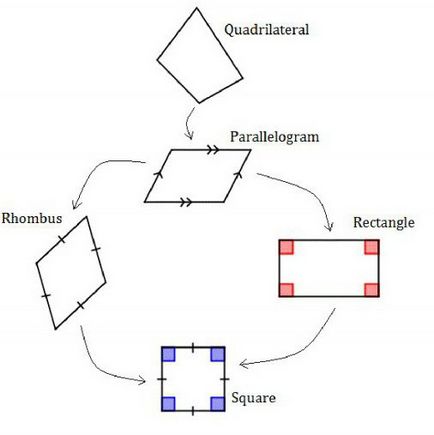
• Klasszikus paralelogramma.
• Rhombus (rombusz) - négyszögletes alakú egyenlő oldalú. Átlók metszéspontja derékszögben, elosztjuk a rombusz négy egyenlő derékszögű háromszög.
• Téglalap (téglalap). Ez a név önmagáért beszél. Mivel ez a téglalap merőlegesen (mindegyik legalább kilencven fok). ellentétes oldalán nem csak párhuzamosak egymással, de egyenlő.
• Square (tér). Mivel a téglalap egy négyszög merőleges, de ő minden oldalról egyforma. Ez, ez a szám közel van egy gyémánt. Tehát azt lehet mondani, hogy a tér - egy kereszt között egy gyémánt és egy téglalapot.

A különleges tulajdonságait a téglalap

Figyelembe véve a számok, amelyekben mindegyik sarka az oldalak közötti egyenlő kilencven fokkal, érdemes közelebbről is összpontosít a téglalapot. Szóval, milyen lehetőségei olyan tulajdonságokkal, amelyek megkülönböztetik a többi paralelogramma?

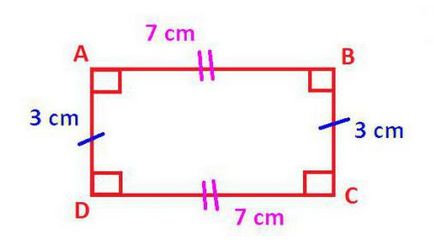
Ahhoz, hogy azt állítják, hogy az alany paralelogramma - egy téglalap, átlók egyenlőnek kell lennie egymással, és az egyes sarkok - egyenes. Ezen túlmenően, a tér a átlók meg kell felelnie a négyzetének összege a két szomszédos oldala az ábrán. Más szóval, a klasszikus téglalap két derékszögű háromszög, azok ismertek, a négyzetének összege a lábak egyenlő a tér a átfogója. A szerepe az átfogó szolgál átlós megfontoltabb négyszög.

Az utolsó ilyen jelei ez a szám is a különleges tulajdonság. Ezen kívül vannak még mások. Például az a tény, hogy minden fél tanult négyszög derékszögben - mind a magassága.

Továbbá, ha egy téglalap köré rajzol egy kört, átmérője egyenlő lesz az átlós a feliratos formában.

Az egyéb tulajdonságok a négyszög, az a tény, hogy az sima és a nem-euklideszi geometria nem létezik. Ez annak a ténynek köszönhető, hogy egy ilyen rendszerben nincs négyszögletes alakja, a szögek összege egyenlő háromszázhatvan fokos.

A tér és jellemzői

Miután foglalkozott a jellemzőit és tulajdonságait a téglalap, akkor kell figyelni, hogy a második ismert a tudomány négyszög merőleges (négyzet).

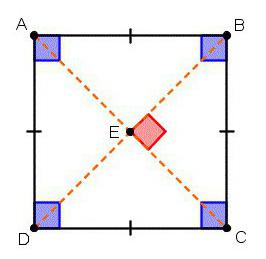
Mivel valójában ugyanaz téglalap, de egyenlő oldalú, ez az alak az összes annak tulajdonságait. De vele ellentétben, a tér van jelen a nem-euklideszi geometria.

Ezen túlmenően, ez a szám, vannak más egyéni jellemzők. Például az a tény, hogy az átlós négyzet nem egyszerűen egyenlő egymással, de metszik egymást derékszögben. Így, mint a rombusz, négyzet amely négy derékszögű háromszögek, amelyben van osztva átlósan.

Ezen túlmenően, ez a szám a legkiegyensúlyozottabb az összes udvarokon.

Mi az az összeg, a szögek egy négyszög

Figyelembe véve a funkciók a négyszögek az euklideszi geometria, meg kell figyelni, hogy a sarkokat.

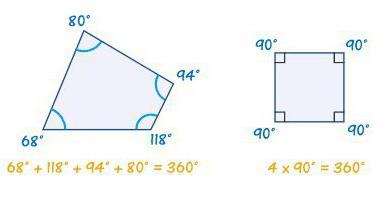
Így minden egyes fenti számok, függetlenül attól, hogy van-e benne vagy sem derékszögben, a teljes összeg ezek mindig ugyanaz - háromszázhatvan fokos. Ez egy egyedülálló tulajdonsága az ilyen típusú számokat.

kerülete négyszögek

Miután foglalkozott, hogy mi az az összeg, a szögek egy négyszög és más speciális tulajdonsága az alakja ezt a fajta, meg kell tudni, hogy mi a legjobb, ha a képletek kiszámításához a kerület és terület.

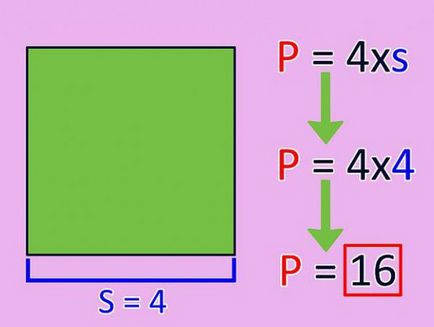
Annak megállapításához, a kerülete bármely négyszög, elég csak add fel egymással a hossza az oldalán.

Például, ábrán KLMN kerülete lehet képlettel számítják ki: P = KL + LM + MN + KN. Ha helyettesíteni itt kapott számok: 6 + 8 + 6 + 8 = 28 (cm).

Abban az esetben, ha a vizsgált ábra - egy négyzet vagy rombusz, megtalálása a kerülete a képletű egyszerűsíteni lehet egyszerűen megszorozzuk a hossza az egyik oldala négy P x = KL 4. példában 6 x 4 = 24 (cm).

Formula négyszögek tér

Miután foglalkozott, hogyan kell megtalálni a kerülete bármilyen alakú, négy oldalát és sarkait, figyelembe kell venni a legnépszerűbb és egyszerű módja a megállapítás a területen.

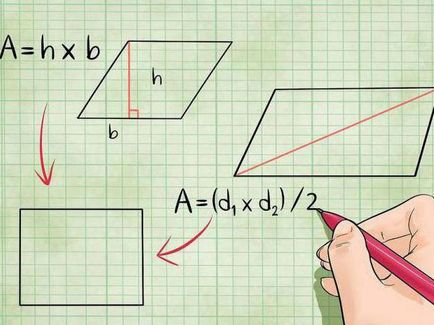
• A klasszikus módja annak kiszámításához - ez az, hogy az általános képletű S = 1/2 × LN KM x SIN LON. Kiderült, hogy adott területen a négyszög felével egyenlő a terméket az átlók a sine a szög található közöttük.
• Ha ez a szám, amelynek területén kell találni - ez egy téglalap vagy négyzet alakú (az átlója, amely mindig azonos egymással), akkor egyszerűsíteni a képlet, emelt téren a hossza egy átlós és megszorozzuk a sine a szög között, és osztjuk ketté minden. Például: S = 1/2 CM 2 x SIN LON.
• Továbbá, ha a terület egy téglalap segítségével a kerület tekinthető a számok és a hossza az egyik oldala. Ebben az esetben ez lesz legcélszerűbb használni a képletben az S = KN x (P - 2 KN) / 2.
  
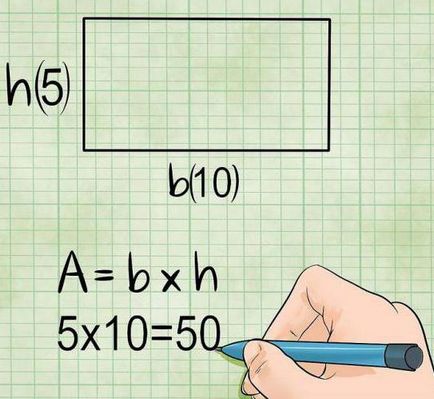
• Abban az esetben, a tér tulajdonságai lehetővé teszik a használatát számos további képletek találni a környéken. Például, ismerve a kerülete alak is alkalmazható ilyen variánst: S = P 2 / 16. És ha az ismert sugara a beírt kör egy négyszög, négyzet terület nagyon hasonló módon: S = 4r 2. Ha a kör sugara ismert, akkor más alkalmas képlet: S = 2R 2. is, a tér területe egyenlő a 0,8 hosszú húzott egyenes a sarokban a szám, hogy a közepén az ellenkező oldalon.
• Amellett, hogy a fenti, is van egy külön képletet találni a területen, kifejezetten a paralelogramma. Ezt fel lehet használni, ha ismert, a hossza a két magasságban a szám, és a mérete a köztük lévő szög. Ezután a magasságot kell szorozni egymással és a szinusz a köztük lévő szög. Érdemes megjegyezni, hogy tudod használni ezt a képletet a számok, amelyek a paralelogramma (azaz, téglalap, rombusz és négyzet).

Egyéb tulajdonságok négyszögből: beírt és körülírt körök

Figyelembe véve a jellemzőit és tulajdonságait a négyszög alakú, mint az az euklideszi geometria, érdemes odafigyelni arra a lehetőségre, hogy leírja a kerek, vagy írja be az alábbi:

• Ha az összeg a szemközti szögek figura által száznyolcvan fokban és egyenlő egymással, lehetséges, hogy leírja egy kört szabadon körül ez négyszög.
• Szerint Ptolemaiosz-tétel, ha a leírt körön kívül sokszög négy oldalán, a termék az átlók összegével egyenlő termékek ellentétes oldalain az ábra. Így, a képlet lenne: cm x LN = KL x MN + LM x KN.
• Ha építeni egy téglalapot, amelynek az összege a szemközti oldalai egyenlők egymással, akkor tudni helyezni egy kört.

Miután foglalkozott azzal a ténnyel, hogy egy ilyen négyszöget, milyen fajta ez létezik, melyek csak derékszögben a felek között, és milyen tulajdonságokkal rendelkeznek, meg kell emlékezni az összes ezt a cuccot. Különösen képletű megtalálása kerülete és területe a sokszögek tekinthető. Végtére is, ez a szám ebben a formában - az egyik leggyakoribb, és ez a tudás hasznos lehet számításokat a valós életben.