Tanulmány a funkció és az építőiparban a grafikon

1) A funkció határozza meg a teljes valós tengelye, azaz a.

2) A metszéspontjai függvény grafikonján a koordináta-tengely.

A metszéspontja. A funkció három pont keresztezi a tengelyek :.

3) a nem-periodikus függvény.

Páratlan funkció, így a grafikont a funkció szimmetrikus az origó.

4) Keresse meg a aszimptotáját a grafikon funkciók. A funkció nincs break pontot, így nincs függőleges aszimptota.

Találunk a lejtőn a asymptote adott

Lejtőn a asymptote sem.

5) Találunk egy szélsőérték funkció és térköz növekvő, csökkenő. Ehhez számoljuk az első derivált

A kritikus pontok, azonosnak az első derivált nulla:

Ezek a pontok osztja a domain négy időközönként. Keresse meg a jel a származékos az egyes intervallumok és az eredményeket sorolja az alábbi táblázatban:

Point - a maximális pontot, a lényeg - a minimális pontot.

6.) Határozza meg a inflexiós pontot, időközönként konvexitás és konkáv. Erre találunk a második derivált

A kritikus pont. Hogy kiegyenlíti ezt a második származékot nullára:

Talált pontot osztja a domain négy időközönként. Találunk a jele a második derivált minden intervallumban, és az eredményeket a táblázatban szereplő:

Az érték a függvény inflexiós pontok

7) A kapott adatok azt ábrázoljuk funkciót.

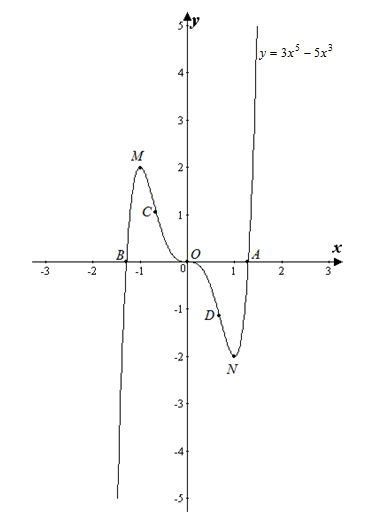
Annak vizsgálatára, a funkció és megépíteni a grafikonon.

1) Határozza meg a domain a funkciót. A függvény egy racionális szám, ezért ki kell zárni az érték nullázódik nevező.

Ez a függvény a tartomány:

2) a grafikon pontjait keresztezi a koordináta tengelyekkel:

Ez a függvény a áthalad a származási - pont.

3) a funkció nem periodikus. Megvizsgáljuk a funkció a paritás:

Egyik egyenletek, vagy sem, így a függvény nem páros és nem páratlan. Függvény grafikonját nem lesz szimmetrikus.

Azon a ponton, törés funkciót. Mi határozza meg a viselkedését egy pont a közelben e pont

Így - az egyenlet vertikális aszimptotákkal.

Találunk a lejtőn a asymptote adott

Kapjuk egyenlet ferde aszimptotákkal.

5) Találunk egy szélsőérték funkciója és tagolása növekedését és csökkenését. Ehhez kiszámítjuk az első derivált, a jogállamiság részleges differenciálódás:

A kritikus pontok: ha

Nincs korlátozás, de ez a pont nem tartozik a domain a meghatározás. Keresse meg a jel a származékos az egyes intervallumok és az eredményeket a táblázatban felsorolt

Ez az a pont - a pont maximum.

6.) Határozza meg a inflexiós pontot, időközönként konvexitás és konkáv. Ehhez találunk a második derivált

A kritikus pontok: ha nem létezik, de ebben a kérdésben nem tartozik a domain meghatározása. Találunk a jele a második derivált minden intervallumban, és az eredményeket a táblázatban szereplő: