Teljes tanulmány a funkció és nyomtatás - studopediya
A teljes tanulmány a funkciók és az építési ütemterv kényelmes elvégzésére az alábbiak szerint:
1), hogy megtalálja a függvény definíciójában terület;
2) meghatározzuk, hogy a funkció nem páros vagy páratlan, időszakos;
3), hogy vizsgálja ki a folytonosság, hogy megtalálja a töréspontot és jellegének tisztázására folytonossági;
4), hogy megtalálja a aszimptotáját a grafikonon;
5) vizsgálja meg a monotonitást, a funkció és megtalálja a szélsőségek;
6) Keresse az inflexiós pont, meg a időközönként konvexitás és konkáv a függvény grafikonját;
7) jelöli a grafikon a további pontokat, például a metszéspont a koordináta-tengelyek.
Az eredmény az egyes elemek tükröződnie kell azonnal a menetrend, és összhangban kell lennie a kutatás eredményei az előző bekezdésekben.
Hogy végezzenek teljes tanulmányt a funkciót, és felhívni a grafikon.
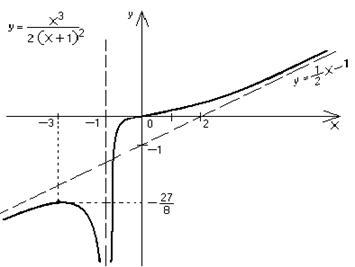
1. A funkció meghatározott intervallumban XÎ (- ¥; 1) È (-1; + ¥).
2. A funkció nem lehet páros vagy páratlan, mert saját domain definíció nem szimmetrikus 0. Így, a funkció az általános formában, azaz, Paritás nem rendelkezik tulajdon. Továbbá, a funkció nem periodikus.
Ez a funkció a még. ha két feltétel teljesül:
a) a domain a meghatározás szimmetrikus nulla,
b) minden x értékei a tartomány közötti egyenlőség.
Graph még függvény tengelyszimmetrikus egy tengely körül OY.
Ez a funkció a furcsa. ha
a) saját domain, a függvény szimmetrikus nulla,
b) ha az „x területén a meghatározás.
Graph páratlan függvény egy központi szimmetrikusan a származás.
A funkció az úgynevezett időszakos. ha van egy szám T> 0 olyan, hogy az egyenlő „x területén a meghatározás.
A szám T az az időszak a függvény. és annak gráf elegendő építésére bármely intervallumban hosszúságú T., majd időközönként terjeszteni az egész tartomány.
3. A függvény folytonos minden xÎ (- ¥; -1) È (-1; + ¥).
Ez a funkció az egység, amely van kialakítva felosztása két folytonos függvények és az alapvető elemi. Ezért az ingatlan folytonos függvények, ez a funkció a folyamatos minden ponton, ahol meg van határozva.
X = -1 ez a pont a törés, mivel benne, ez a funkció nem meghatározott. Annak megállapításához, a természet (típus) a rés, kiszámításához. Következésképpen x = -1 funkció végtelen diszkontinuitás (II nemzetség rés).
4. aszimptotája a grafikon funkciók.
Függőleges aszimptota az a vonal, X = -1 (ez következik törés kutatási funkciója).
Ferde asymptote keres egyenlet. ahol
Így, - ez az egyenlet ferde aszimptotákkal (a H® ± ¥).
5. A monotónia és szélsőséges funkciójának meghatározása segítségével az első deriváltját:
A kritikus pont határozza meg a következő feltételek:
Elégséges feltételei a monotonitás és a szélsőértékek:
6. időközönként domborulat van és konkáv a grafikon, annak inflexiós pont használja a második derivált:
Gyanús a inflexiós pont határozza meg a következő feltételek:
Elégséges feltételei konvexitás, konkáv és inflexiós pontok:
O pont (0, 0) az inflexiós pont a grafikon.
kutatási eredmények gyakran működnek segítségével az első és második derivált készít általános táblázatot a fő tulajdonságait a grafikont a funkció:
Minden a kutatási eredmények függvényében tükrözi ütemtervet.
OOF: XÎ (- ¥; -) È (-;) È (; + ¥).
Ez egy páratlan funkciója, mint a dómén szimmetrikus nulla és „x Î OOF egyenlőség:
Ezért a függvény grafikonját központi szimmetrikusan a származás.
A függvény folytonos minden xÎ (- ¥; -) È (-;) È (; + ¥), mint elemi függvény folytonos annak OOF. X = - = és x pontok végtelen diszkontinuitás, mert
Függőleges aszimptotájának a grafikon a vonalak X = - és X =.
Ferde asymptote :. ahol
- ez az egyenlet ferde asymptote.
Időközönként növekedését és csökkenését a függvény, a szélsőséges.
Feltétel Extrema:
Elégséges feltételei a monotonitás és a szélsőértékek:
Periódusai konvexitás, konkáv a függvény grafikonját és az inflexiós pontot:
A x = 0 a inflexiós gyanús.
O pont (0, 0) egy inflexiós pont.
Egész táblázat a főbb tulajdonságait a grafikonon ezt a funkciót be lehet állítani csak az xÎ [0; + ¥) következtében a központi szimmetria grafikon pont (0; 0):