ütemezés funkció

Függvény grafikonját.

Mi választjuk ki a gépet derékszögű koordináta-rendszert, és a telek abszcissza értékét az érvelés x. és az ordináta tengelyen - értékét a függvény y = f (x).

A grafikon a függvény y = f (x) a készlet minden pontot abszcisszájú tartoznak a domain a funkció, és az ordináta értékek megegyeznek a megfelelő funkciót.

Más szóval, a függvény grafikonját y = f (x) - a készlet minden pont a síkon, a koordinátái x, y kielégíti a következő összefüggést y = f (x).

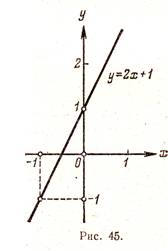
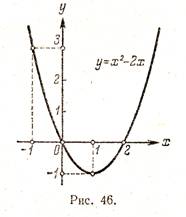
Ábra. 45. és 46. ábra egy grafikon, a 2x + y = 1, és y = x 2 - 2x.

Szigorúan véve, az egyik meg kell különböztetni a függvény grafikonján (a pontos matematikai definícióját, amelyet a fent megadott), és húzott egy görbe, amely mindig ad egy többé-kevésbé pontos vázlatot a grafikonon (és még akkor is, mint általában, nem csak grafika, de csak egy része található a végső rész sík). A jövőben azonban akkor általában azt mondják „menetrend”, és nem „a vázlat grafika.”

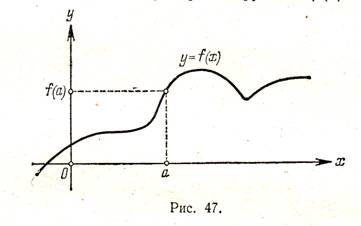
A menetrend megtalálható a függvény értékét azon a ponton. Nevezetesen, ha a pont x = a tartomány a függvény y = f (x). majd számának meghatározására f (a) (m. f. függvény értékei x = a) kell megtenniük. Kell át a ponton abszcissza x = a felhívni a párhuzamos egyenes az y-tengelyen; ez a vonal metszi az grafikon y = f (x) egy ponton; ordináta E pont lesz, definíció szerint grafika, megegyezik az f (a) (ábra. 47).

Például, egy f (x) = x 2 - 2x keresztül grafika (. Ábra 46) kapjuk f (-1) = 3, F (0) = 0, F (1) = -l, F (2) = 0 és t. d.

Funkció grafikon szemlélteti a viselkedését és tulajdonságait a funkciót. Például, a ábra. 46 egyértelmű, hogy a függvény az y = x 2 - 2x veszi pozitív x értéke <0 и при х> 2. negatív - 0

A konstrukció a grafikont a f (x), hogy megtalálja az összes pontot a sík, a koordinátái x, y, amelyek megfelelnek az egyenlet y = f (x). A legtöbb esetben ez nem lehetséges, mivel egy ilyen végtelen számú pontot. Ezért a grafikon kb ábrázolják - kisebb vagy nagyobb pontosság. A legegyszerűbb módszer korrekt több pontot. Ez abból áll, hogy az az érv x ad véges számú értékek - mondjuk, x1. x2. x3. xk és töltsük fel asztalra, amely magában foglalja az értéke a kiválasztott funkció.

Táblázat az alábbiak szerint:

A megfelelő öt pont ábrán mutatjuk be. 48.

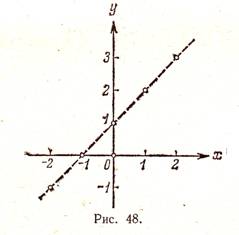
Alapján a helyét e pontok arra a következtetésre jutottak, hogy a függvény grafikonját egy egyenes vonal (ábra. 48 szaggatott). Meg tudjuk ezt a következtetést megbízható-e? Ha nincs további érveket, hogy támogassa ezt a következtetést, aligha tekinthető megbízhatónak. megbízható.

Hogy támasztja alá állítását, úgy a függvény

A számítások azt mutatják, hogy az értékek ennek a funkciónak a pontokon -2, -1, 0, 1, 2 csak a fent leírt táblázat. Azonban, a grafikon az ez a funkció nem egy egyenes vonal (ábrán látható. 49). Egy másik példa az y = x + l + sinπx; értéke is le van írva a fenti táblázatban.

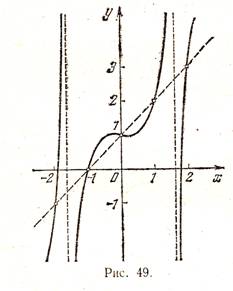
Ezek a példák azt mutatják, hogy a „tiszta” formában módszer rajzoló több megbízhatatlan pont. Ezért, hogy össze egy adott funkció chart, általában a következőképpen kell eljárni. Eleinte tanulmányozása tulajdonságait ezt a funkciót, amellyel meg lehet építeni egy menetrend vázlat. Ezután kiszámítjuk a függvény értékei több ponton (a választás függ a tulajdonságait a funkció be van állítva) generálja a megfelelő pontot. Végül, a felvitt pontokat hajtjuk görbe, a tulajdonságok használatával a függvény.

Néhány (a legegyszerűbb és leggyakrabban használt) tulajdonságait funkciókat használnak megtalálása grafikai vázlat, nézzük meg később, de most vizsgálja néhány általánosan használt módszerek grafikon.

A grafikon y = | f (x) |.

Az egyik gyakran építeni függvény grafikonját y = | f (x) |, ahol f (x) - egy adott funkciót. Emlékezzünk, hogyan kell ezt csinálni. A meghatározás szerint az abszolút értéke a szám felírható

Ez azt jelenti, hogy a grafikon y = | f (x) | lehet beszerezni a telek, az y = f (x) a következő: az összes pontot a függvény grafikonját y = f (x). akinek ordináta nem negatív, akkor el kell fogadni; Továbbá, ahelyett, hogy a grafikon a pontok y = f (x). negatív koordinátákat kell építeni a megfelelő pont a függvény grafikonját y = -f (x) (m. e. részét a függvény grafikonját
y = f (x). hogy alatt fekszik az X tengely, meg kell jelennie szimmetrikusan az x tengely).

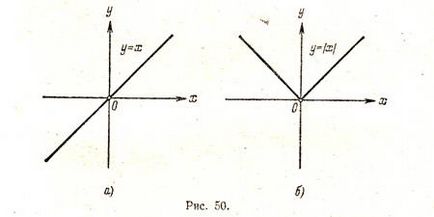
2. példa Szerkesszünk egy olyan grafikont a y = | x |.

Vesszük a függvény grafikonját y = x (ábra. 50 a), és része a grafikon x <0 (лежащую под осью х ) симметрично отражаем относительно оси х. В результате мы и получаем график функции у = |х| (рис. 50, б).

3. példa Plot a függvény az y = | x 2 - 2x |.

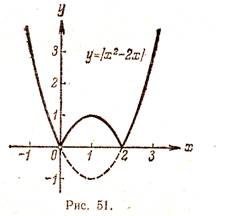
Először is össze egy grafikon y = x 2 - 2x. A grafikon az ezt a funkciót - parabola ágai, amelyek felfelé, a csúcsa a parabola a koordinátái (1, -1), a grafikon metszi az x tengely a pont 0 és 2. a (0, 2) fuktsii veszi negatív értékeket, így ez a része a grafikon tükrözi szimmetrikusan az abszcissza. A 51. ábra azt ábrázolja a függvény az y = | x 2 -2x |. a grafikon alapján a függvény az y = x 2 - 2x

A grafikon y = f (x) + g (x)

Tekintsük a probléma az épület a grafikon y = f (x) + g (x). hacsak grafikus funkciók y = f (x) és y = g (x).

Megjegyezzük, hogy a domain a funkció y = | f (x) + g (x) | Ez a készlet az említett értékek x esetében, amelyek meghatározott funkció mind y = f

Tegyük fel, hogy pontokat (x0. Y1), (x0. Y2) rendre tartoznak chart funkciók y = f és y = g (x). t. e. y1 = f (x0), y2 = g (x0). Ezután a pont (X0;. Y1 + y2) tartozik a grafikon y = f (x) + g (x) (f (x0) + g (x0) = y1 + y2). ahol bármelyik pontján a grafikon y = f (x) + g (x) lehet így kapott. Következésképpen, a függvény grafikonját y = f (x) + g (x) lehet beszerezni a grafikonok y = f (x). és y = g (x) helyett minden pontja (xn. y1) grafikonja y = f (x) pont (xn. y1 + y2), ahol Y2 = g (xn), m. e. elmozdulás minden pontjában (xn. y1) a grafikon y = f (x) mentén az y-tengelyen az összeg a y1 = g (xn). Itt csak azokat pontokat Xn meghatározásra, amelyre mind a függvény az y = f (x) és y = g (x).

Ilyen ábrázoljuk az y = f (x) + g (x) nevezik módszer hozzáadásával grafikonok y = f (x) és y = g (x)

4. példa Az ábrán hozzáadásával a grafikonok ábrázoltuk funkció
y = x + sinx.

Az építőiparban a grafikon y = x + sinx, azt feltételeztük, hogy az f (x) = x, és g (x) = sinx. A konstrukció a grafikon kiválaszt egy pontot abtsissami -1,5π, -, -0,5, 0, 0,5, 1,5, 2. Az értékek az f (x) = x, g (x) = sinx, y = x + sinx Számítsuk kiválasztott pontokon, és az eredményeket kerülnek egy táblázatot.