Vektorok és műveletek vektorokkal

A szabvány meghatározza a „vektor - egy irányított szegmens." Jellemzően ezek korlátozottak, és végzős ismerete vektorok. Kinek van szüksége egy kis „irányított szegmensek?

És valóban, hogy az ilyen vektorok és miért is?
Időjárás előrejelzés. „Wind északnyugatra, sebessége 18 méter másodpercenként.” Egyetértenek abban, hogy van nagyságát és irányát a szél (ahol a szél fúj), és a modul (vagyis az abszolút értéke) a sebességet.

Az értékek nem egy irányba, az úgynevezett skalár. Mass, a munka, az elektromos töltés nem irányul. Jellemzőjük a számérték - „hány kilogramm” vagy „hány joule.”

Fizikai mennyiségek, amelyek nem csak az abszolút érték, hanem az irányt nevezzük vektor.

Sebesség, erő, gyorsulás - vektorok. Számukra fontos, hogy „mennyire” fontos „ahol”. Például, a nehézségi gyorsulás irányul a Föld felszínén, és értéke egyenlő 9,8 m / s 2. Az impulzusszélesség elektromos mező, a mágneses mező - az azonos vektort mennyiségeket.

Eszedbe fog jutni, hogy a fizikai mennyiségek által kijelölt leveleket, latin vagy görög. A nyíl a fenti levél azt mutatja, hogy a nagyságát a vektor:

Itt egy másik példa.
Az autó mozog A-ból B A végeredmény - ez mozgatja a pont-pont B. mozgás, azaz a vektor.

Most már értem, hogy miért a vektor - egy irányított szegmensben. Felhívjuk figyelmét, hogy a végén a vektor - ahol a nyíl. A hossza a vektor hossza ebben a szegmensben. Jele: vagy

Eddig dolgoztunk együtt skalárnak, a szabályok szerint az aritmetika és az elemi algebra. Vektor - egy új koncepció. Ez egy másik osztály matematikai objektumok. Számukra a szabályokat.

Miután a szám nem tud semmit. Megismerni őket kezdődött a korai évfolyamokon. Azt találtuk, hogy a számokat össze lehet hasonlítani egymással, összeadni, kivonni, szorozni és osztani. Megtudtuk, hogy van egy egységek számát és a nullát.
Most be vektorokkal.

A fogalmak „több” és „kevesebb, mint” vektorok nem léteznek -, mert a saját irányítása eltérő lehet. Akkor csak összehasonlítani a hossza a vektor.

De az egyenlőség fogalma vektorok ott.
Egyenlő egy vektor, amely azonos hosszúságú, és ugyanabban az irányban. Ez azt jelenti, hogy a vektor átvihető önmagával párhuzamosan bármely pontján a sík.
Az egység egy olyan vektor, amelynek hossza egyenlő 1 Nulla - vektor, amelynek hossza egyenlő nullával, vagyis annak eredetét egybeesik a végén.

A legkényelmesebb módja, hogy működjön együtt a vektorokat a derékszögű koordináta-rendszerben - ugyanaz, ahol a sorsolás grafikonok a funkciók. Minden pont a koordináta-rendszerben megfelelnek az két szám - koordinátáit x és y. abszcissza és ordináta.
Egy vektort is, amelyet két koordináta:

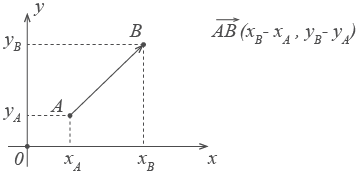
Itt zárójelben rögzített koordinátákat a vektor - az x és y.
Ezek egyszerűen: koordinátája a végén a vektor mínusz koordináta fogva.

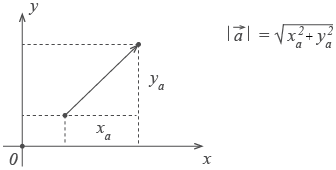
Ha a koordinátákat a vektor kapnak, hossza adják

hozzáadásával vektorok

Vektor kívül van két módon.

1. Szabály paralelogramma. Szeres vektorok és mindkét Start egy ponton. Ahhoz, hogy befejezzék a paralelogramma és ugyanazon pontján az átlós a paralelogramma végre. Ez lesz az összeg a vektorok.

Ne feledje, a mese egy hattyú, a rák és a csuka? Megpróbálták nagyon nehéz, de nem mozdult a helyén WHO. Miután a vektort erők összege az általuk alkalmazott, hogy a kocsi, akkor nulla.

2. A másik módszer az vektorok - általában háromszög. Vegyük a vektorok. Végére az első vektor csatolja az elején a második. Most össze a kezdete az első és a második végén. Ez az összeg a vektorok.

Ugyanabban egy szabály szerint lehet hajtani, és több olyan vektor. Csatolni őket egyesével, majd csatlakoztassa az elején az első végén az utóbbi.

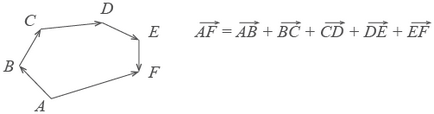
Képzeld el, hogy megy a pont-pont B. B-től C C D akkor E és F. A végeredmény Ezen intézkedések - a mozgó-tól F

Ha hozzá vektorok és megkapjuk:

kivonása vektorok

Vektor irányul szemben a vektor. A hossza a vektorok és egyenlő.

Most már egyértelmű, hogy ez a kivonás vektorok. A különbség vektorok és - ez az összeg a vektor és a vektort.

Szorzás vektor számos

Amikor szorozva száma a vektor k egy vektor k hosszúságú idő eltér a hossza. Ő ugyanabban az irányban a vektorral, ha k értéke nullánál nagyobb, és ellentétes irányú, ha k értéke nullánál kisebb.

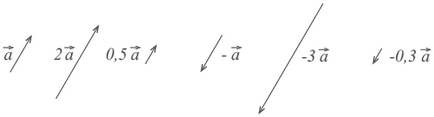
Meg is találta, amit keresett? Ossza meg ezt a barátaiddal!

A skaláris szorzata két vektor

Vektor lehet szorozni nem csak számokat, hanem egymást.

Skaláris termék a termék hosszának a vektorok által koszinusza a köztük lévő szög.

Felhívjuk figyelmét -, hogy szaporodnak két vektor skalár és megfordult, hogy az a szám. Például, a fizika, a mechanikai munka egyenlő skalár szorzata két vektor - az erők és mozgalmak:

Ha a vektorok merőleges, a skalár szorzat nulla.
És ez fejeződik ki skalár szorzata vektorok és koordináták:

Megtalálható a szöget a vektorok a képletet a belső termék:

Ez a képlet különösen hasznos szilárd geometria. Például, a probléma a C2 kell találni a szöget az egyenes vagy ferde közötti egyenes és sík. Gyakran előfordul, hogy a vektor C2 eljárás probléma megoldódik néhány szer gyorsabb, mint a klasszikus.

Az iskolai tananyag matematika tanulmányi csak skaláris szorzata vektorok.
Kiderült, kivéve a skalár, van is egy vektor a terméket, mert a szorzás eredményét két vektor egy vektor. Ki szállít a vizsga fizika. tudja, mi a Lorentz-erő és a Ampere erő. A képlet a megállapítás ezek az erők nevezetesen vektor termékek.

Vektor - hasznos matematikai eszköz. Ebben látni fogja az első évben.

Hívjon minket: 8 (800) 775-06-82 (Magyarországon belül ingyenesen hívható) +7 (495) 984-09-27 (ingyenesen hívható Moszkva)

Vagy kattintson a „További információ”, hogy töltse ki az űrlapot. Mi biztosan visszahívlak.