Mi a vektor

Vektor - egy matematikai objektum, amelyet az jellemez, irányát és nagyságát. A geometria a vektort nevezzük vonalszakasz egy síkban vagy térben, amely egy meghatározott irányban, és hossza.

kijelölés vektor

Jelölésére alkalmazott vektorban egy vagy két kisbetűs tőke,

amelyek megfelelnek a kezdetét és végét egy vektor, vízszintes vonal képviseli ebben az esetben több mint a betűket. Az első betű jelzi a kezdetét a vektor, a második - a végén (lásd: 1. ábra). A grafikus kijelző a vektor képviseli egy nyíllal annak irányát.

Mik a koordinátákat a síkban és a térben?

A koordináták a vektor - ez csak egy lehetséges együtthatói lineáris kombinációja alapján vektorok a választott koordinátarendszerben. Úgy hangzik, bonyolult, de valójában igen egyszerű. Nézzük a következő példát.

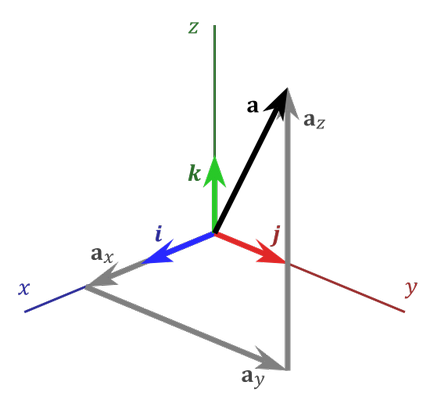
Tegyük fel, hogy meg akarjuk találni a koordinátákat a vektor. Tegye egy háromdimenziós koordináta-rendszer (lásd. 2. ábra), és hajtsa végre a vetülete a vektor az egyes tengelyeken. Vektor és ebben az esetben a következőképpen írható fel: A = ax i + ay j + AZ k, ​​ahol az i, j, k - alapján vektorok, ax. ay. AZ - együtthatók, amelyek meghatározzák a koordinátákat a vektor egy. Az expressziós fogják hívni lineáris kombinációjával. A sík (derékszögű koordináta-rendszert) lesz lineáris kombinációja a két bázisok és együtthatókat.

kapcsolat vektorok

Elméletileg van vektorok egy olyan kifejezés, mint hozzáállás vektorok. Ez arra utal, hogy a megállapodás a vektorok egymáshoz síkban és térben. A leghíresebb különleges esetekben kapcsolatok vektorok:

• kollinearitás;
• Az igazítás;
• coplanarity;
• egyenlőséget.

Kollineáris vektorok egy egyenesbe esik, vagy egymással párhuzamosan, azonos jellemző vektorok codirectional irányba síkba esik - egy olyan elrendezés, ugyanabban a síkban, vagy párhuzamos síkokban, egyenlő a vektor azonos irányú és hosszát.