Rugalmassága funkció - studopediya
Származékai magasabb rendű
Mivel a függvény deriváltját maga egy funkciót, akkor is levezethető. A koncepció a származék, amelyet a fentiekben tárgyaltuk, utal egy származékát az elsőrendű.
Deriváltja az n-edik érdekében a származék a-származék
(N - 1) -edik érdekében. Például F `` (x) = (f `(x))` - a származékot másodrendű (vagy második derivált), f `` `(x) = (f`` (x)) `- a származékot a harmadik végzést (vagy harmadik származék), stb Néha jelölésére származékok magasabb rendű használnak római vagy arab számokkal zárójelben, például F (5) (x) vagy f (V) (x) az ötödrendű származékot.
A fizikai jelentése magasabb rendű származékok meghatározott ugyanúgy, mint az első származékot: mindegyik jelentése a változás mértéke származékot az előző sorrendben. Például, a második derivált változásának sebessége az első, azaz a sebességű aránya. Egyenes vonalú mozgást ez a gyorsuló időpontban.
Rugalmasság funkció Ex (y) nevezzük határa az arány a relatív növekmény a függvény relatív növekmény az érvelés x, az utolsó nullához :.
Rugalmasság funkció megmutatja kb, a százalékos változás függvény az y = f (x) a független x változó változik 1%.
Gazdasági szempontból, a különbség az index a származékot, hogy a származék a mértékegységet, és így, annak értéke függ az egységek, amelyben a mért változó. Például, ha a függőség a termelés az időt is tonnában kifejezve, illetve, és hónap, a származékos megmutatja a határ növekedése tonna havonta; ha az intézkedés e mutatók, például kilogrammban, és a napokban, és a funkciót is, és annak származékai más lesz. A rugalmasság is eredendően dimenziómentes mennyiség (mért százalékos vagy frakciók), és így nem függ a skálán arányok.
Alapvető tételek a differenciálható függvények és alkalmazásaik
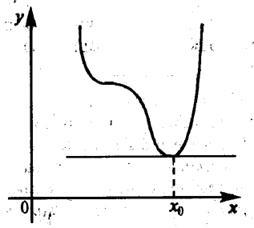
Fermat-tétel. Ha az intervallum differenciálható függvény eléri a legmagasabb vagy a legalacsonyabb érték a belső pont a végét, a függvény deriváltját ezen a ponton nulla.
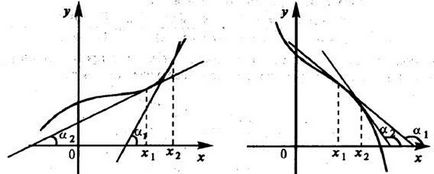
A geometriai jelentése Fermat-tétel abban a tényben rejlik, hogy a ponton a legnagyobb vagy legkisebb elért érték belsejében az intervallum, az érintő párhuzamos a grafikon abszcissza (3.3 ábra).
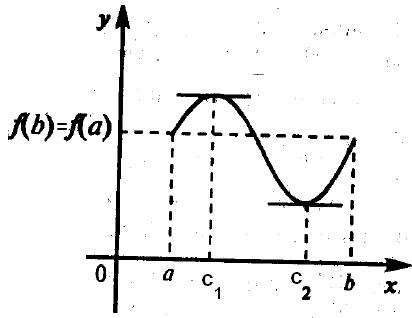
Rolle-tétel. Legyen a függvény az y = f (x) teljesíti a következő feltételeket:
1) folytonos a [a, b];
2) differenciálható időközönként] a, b [;
3) a végpontokon egyenlő értékeket, azaz, f (a) = f (b).
Ezután, a szegmensen belül létezik legalább egy pont, ahol a származék funkció nulla.
A geometriai jelentése tétel Rolle, hogy létezik legalább egy pont, ahol az érintő a grafikon x-tengely párhuzamos a (például a 3.4 ábrán két ilyen pont).
Ha f (a) = f (b) = 0, Rolle tétel lehet azt más módon, két egymást követő nulla differenciálható függvény legalább egy nulla a származék.
Rolle-tétel egy konkrét esetben a Lagrange-tétel.
Lagrange-tétel. Tegyük fel, hogy a függvény az y = f (x) teljesíti a következő feltételeket:
1) folytonos a [a, b];
2) differenciálható időközönként (a, b).
Azután az szegmens van legalább egy ilyen pontot, a kdtoroy származékot egyenlő a hányadosa a növekmény a funkciót a növekmény az érvelés ebben a szegmensben :.
Ahhoz, hogy megértsük a fizikai értelmében a Lagrange-tétel, azt látjuk, hogy nincs több, mint az átlagos változás mértéke funkciót a [a, b]. Így a tétel azt mondja, hogy a szegmensen belül van legalább egy pont, amelynél a „pillanatnyi” változási sebessége a funkció megegyezik az átlagos változás mértéke a teljes szegmensben.
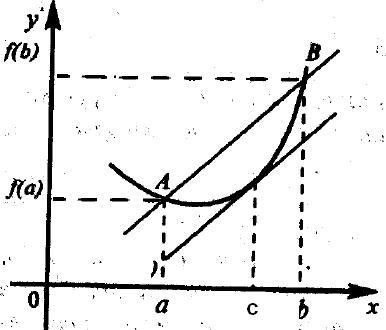
A geometriai jelentését Lagrange-tétel szemlélteti a 3.5 ábrán látható. Megjegyezzük, hogy a kifejezés egy egyenes meredeksége, amelyen fekszik a húrt AB. A tétel kimondja, hogy a függvény a grafikon, létezik legalább egy pont, ahol az érintő hozzá párhuzamos a húrt (azaz, a lejtőn a tangens - származékot - ugyanaz lesz).
Következmény: ha a derivált nulla néhány intervallumon, akkor a függvény azonosan konstans ezen intervallumban.
Tény, hogy ezen [a, b] intervallum [a, x]. Lagrange-tétel ebben az intervallumban van egy pont, amelyre. Ennélfogva F (a) - f (x) = f `(a) (a - x) = 0; f (x) = f (a) = const.
L'Hospital-szabály. A határérték az arány a két végtelenül kicsi vagy végtelenül nagy funkciók egyenlő a határ az arány azok származékai (véges vagy végtelen), amennyiben ez utóbbi létezik ebben az értelemben.
Más szóval, ha van bizonytalanság az űrlapot, majd.
Alkalmazása L'Hospital-szabály, hogy megtalálják a határt, hogy felül kell vizsgálni a gyakorlati órák.
A elégséges feltétele növekvő (csökkenő) függvény. Ha a differenciálhányados differenciálható pozitív (negatív) egy bizonyos időn belül, akkor a funkció növeli (csökkenti) ebben az intervallumban.
Bizonyítás. Tekintsük a két érték x1 és x2 egy adott intervallumban (mondjuk x2> x1). By tétel LaGrand on [x1. x2] van egy pont, ahonnan. Ezért f (x2) - f (x1) = f `(c) (x2 - x1). Ekkor F `(c)> 0, a bal oldali egyenlőtlenség pozitív, vagyis az, f (x2)> f (x1), és a funkciót növekszik. Ha az F-`(c) <0 левая часть неравенства отрицательна, т.е. f(х2 )
A geometriai értelmezése funkció monotonitási feltételek: ha a érintő a görbe egy bizonyos időközönként orientált hegyes szögben a vízszintes tengely, a funkció növeli, és ha a tompaszög, akkor csökken (lásd a 3.6 ábra.).
Megjegyzés: A előfeltétele a monotónia a gyengébb. Ha a funkció növeli (csökkenti) egy bizonyos időközönként, majd ezt a származékot nem-negatív (nem pozitív) ebben az intervallumban (azaz különböző pontjain származék monoton függvény lehet nulla).