Vektorok és műveletek vektorokkal

Vektor különleges helyet foglalnak el tárgyak között tartják magasabb matematika, hiszen minden vektor nemcsak egy számérték - hossza, hanem a fizikai és geometriai - orientáció. A vektor által képviselt irányított vonalszakasz terjedő az A pont a B. pontban jelöljük.

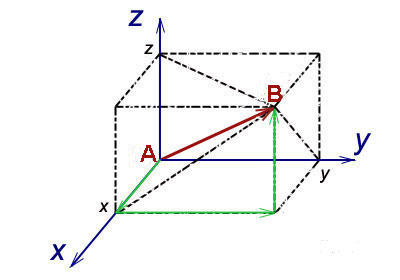
Vektor - egy olyan típusú ábrázolása azt a pontot, amelyhez hozzá kell férni néhány kiindulási pont. Például, egy három dimenziós vektor, általában írott formában (x, y, z). Beszéd egészen egyszerűen azok a számok azt jelentik, hogy meddig akarsz menni három különböző irányban, hogy a lényeg.

Adott egy vektor. Ahol X = 3 (jobb karját jobbra mutató), y = 1 (bal kéz mutató előre), Z = 5 (pont alatt áll vezető lépcső). Ezekből az adatokból, talál egy pontot az elhaladó 3 méter által jelzett irányba a jobb kezét, majd 1 méteres által jelzett irányba a bal kezével, majd vársz egy létrát, és felkapaszkodott 5 méter, akkor, végül is a kívánt ponton.

Minden más szempontból - pontosabb magyarázatot fent bemutatott szükséges különböző műveletek vektorok, azaz a gyakorlati problémák megoldására. Séta ebbe szigorúbb definíció, utalva a tipikus feladatok a vektorok.

Fizikai példák vektor mennyiségek szolgálhat elmozdulása egy anyagi pont, mozgó térben, sebesség és gyorsulás ezen a ponton, valamint ható erejét.

A geometriai vektort képviseli a kétdimenziós és a háromdimenziós tér, mint egy irányított vonalszakasz. azaz szegmens, amelyek megkülönböztetik az elején és végén.

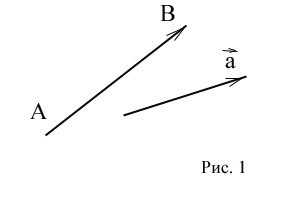
Ha A - az elején a vektor, és a B - annak végén, a vektor jelöli egy vagy kis levelet. Az ábra azt mutatja, a végén a vektor nyíl (ábra. 1)

Hossz (vagy modult) a hossza a geometriai vektor generálásához hossza

Két vektor azt mondják, hogy egyenlő. ha lehet kombinálni (a koincidencia irányban) által párhuzamos átvitel, azaz a ha azok párhuzamosak, ők irányítják egy és ugyanabban az irányban, és az azonos hosszúságú.

A fizikában gyakran tekintik foglalt vektorok. előre meghatározott ponton az alkalmazás, hosszúságú és irányú. Ha az alkalmazás helyétől a vektor nem számít, akkor is át, miközben a hossza és iránya a tér bármely pontján. Ebben az esetben, a vektor úgynevezett szabad. Egyetértünk abban, hogy fontolja meg csak a szabad vektorok.

Szorzás vektor számos

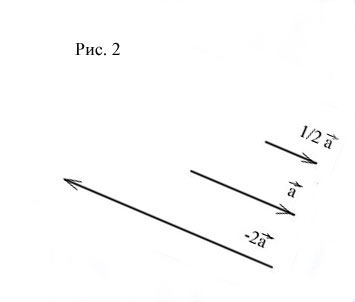
Vektorana termék szám egy vektor, a vektorokból származó nyújtás (ha), vagy egy összehúzódást (miközben) időben, az irányt a vektor mentett ha és fordított, ha. (Ábra. 2)

A definíció következik, hogy a vektorok u mindig található az azonos vagy párhuzamos vonalak. Az ilyen vektorok nevezzük kollineáris. (Azt is lehet mondani, hogy ezek a vektorok párhuzamosak, de a vektor algebra mondani, hogy „egyenesbe”.) Fordítva is igaz: ha a vektorok és egyenesbe esik, akkor kapcsolja össze

Ezért, (1) egyenlet fejezi ki feltétele kollinearitása két vektor.

Összeadás és kivonás, vektorok

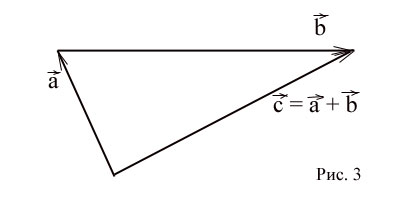
Ha hozzá vektorok tudniuk kell, hogy az összeg a vektorok egy vektor, kezdetét, amely egybeesik az elején a vektor, és a végén -, hogy a végén a vektor, feltéve, hogy az eredete a vektor alkalmazható a végén a vektor. (Ábra. 3)

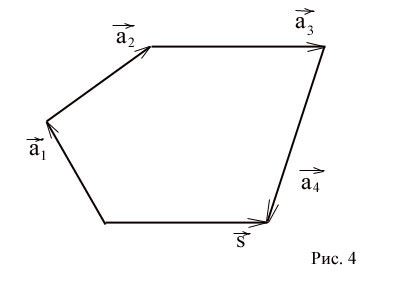
Ez a meghatározás lehet felosztani bármely véges számú vektorok. A térben n szabadon vektorok. Ha hozzá több vektorok figyelembe az összegük NO vektor, amelynek a kezdete egybeesik az elején az első vektort és a végén - a végén az utolsó vektor. Azaz, ha a végén a vektor, hogy a start vektort és a végén a vektor - az elején a vektor, stb és végül, a végén a vektor - az elején a vektor, ezek összege vektorok záró vektor kezdetét, amely egybeesik az elején az első vektort és a végén - a végén az utolsó vektor. (Ábra. 4)

A kifejezések nevezzük komponensei a vektor, és a megfogalmazott szabály - a szabály a sokszög. A sokszög nem lehet lapos.

Amikor szorozva a vektorok számát kapott -1 ellenkező vektor. Vektorok azonos hosszúságú, és ellentétes irányban. Ezek összege adja a nulla vektor. amelynek hossza egyenlő nullával. nulla vektor iránya nincs meghatározva.

A vektor algebra nem kell figyelembe venni külön kivonás: kivonni a vektor olyan vektor, adunk a szemközti vektor a vektor, vagyis

1. példa: Egyszerűbb a kifejezés:

azaz, vektorok lehet adni, és számának szorzata, valamint polinomok (különösen, a probléma is, hogy egyszerűsítse a kifejezéseket). Jellemzően, a szükségességét, hogy egyszerűsítse a lineáris kifejezések ilyen vektorok előtt következik be számítástechnikai termékek vektorok.

2. példa Vektorok és szolgálja átlói az ABCD paralelogramma (4a.). Kifejezve a vektorok, és amelyek részesei e paralelogramma.

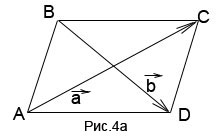
Határozat. A metszéspontja az átlók a paralelogramma osztja minden átlós fél. A hossza a kívánt vektorok közül vagy mindkettő fele összege vektorok alkotó háromszög a kívánt vagy mint különbség fele (attól függően, hogy az irányt szolgáló átlós), vagy, az utóbbi esetben, a fele az összeget, hozott a mínusz jel. Így a szükséges vektorok:

Hogyan lehet megtalálni a hossza az összeg a vektorok?

Ez a probléma egy különleges helyet foglal el a műveletek vektorokkal, mivel magában foglalja a trigonometrikus tulajdonságait. Tegyük fel, hogy rátaláltam a probléma, mint a következő:

Mivel a hossza a vektor és a hossza az összeg ezen vektorok. Keresse meg a hossza közötti különbség ezen vektorok.

Az ilyen és más hasonló problémák, és a magyarázata, hogy a problémák megoldására - a leckét „kiegészítés vektorok: vektor összege a hossz és a koszinusz tétel”.

És nézd meg a megoldás az ilyen problémákra is látható a kalkulátor online „ismeretlen oldalán egy háromszög (Emellett a vektorok és a koszinusz tétel).”

Amennyiben a termékeket vektorok?

A termék egy vektor-vektor nem lineáris műveleteket, és külön is. És megtanultuk „skalár termék vektorok” és „vektor és a vegyes termék vektorok”.

A vetítés a vektor tengelye megegyezik a termék a hossza a vetített vektor a koszinusza közötti szög a vektor és a tengely:

Mint ismeretes, egy vetülete az A pont az egyenes vonal (sík) van a láb a merőleges ettől a ponttól, hogy a vonal (sík).

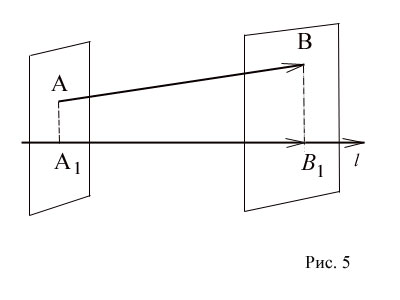
Let - tetszőleges vektor (5. ábra), és és - előrejelzések annak megkezdését (A pont), és a végén (B pont) a L-tengely. (Építésére a nyúlvány A pont) a vonalon keresztül pont végző sík merőleges vonal. A metszéspontja vonal és sík határozza meg a kívánt vetítés.

L vektorana tengely komponenst nevezzük vektor feküdt a tengelyen, az elején, amely egybeesik a vetülete a kezdete és vége - a végén a vektor vetítés.

A vetítés a vektor az L-tengely száma

vektor hossza megegyezik a tengelyre, együttesen a plusz jel, ha sostavlyayushey iránya egybeesik a tengely irányában l. és negatív előjellel, ha azok ellentétes irányban.

A fő tulajdonságai a vektor nyúlványok a tengelyen:

1. A nyúlványok vektorok egyenlő egy és ugyanazon tengely egyenlő.

2. Amikor szorozva száma vektor vetítési szorozni ugyanazt a számot.

3. A vetítés a vektor összeg bármely tengely összegével egyenlő a nyúlványok azonos feltételek tengely vektorok.

4. A vetítés a vektor tengelye megegyezik a termék a hossza a vetített vektor a koszinusza közötti szög a vektor és a tengely:

Példa 3. Számítsuk ki a vektor összege vetülete a L-tengely. ha és sarkok -

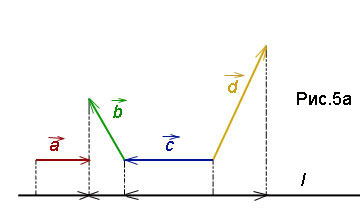
Határozat. L projekt a vektorok a fent meghatározott elméleti segítséget tengelyen. Tól fig.5a nyilvánvaló, hogy a nyúlvány a vektor összege egyenlő az összege a nyúlványok a vektorok. Kiszámítjuk ezen előrejelzések:

Találunk a szükséges vetítési vektor összege:

Ismerete Descartes-féle derékszögű koordináta-rendszer a térben tartott a megfelelő osztályra. kívánatos, hogy nyissa meg egy új ablakban.

A megrendelt rendszer Koordinátatengelyek 0xyz Ox tengely nevezik a vízszintes tengely. 0y tengely - y-tengely. és a tengely 0z - z-tengely.

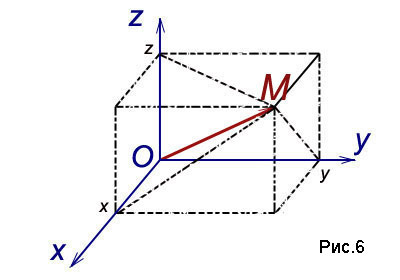
Egy tetszőleges ponton M társult térvektor

az úgynevezett sugár vektor az M pont és vetíteni az egyes koordinátatengelyeken. Jelöljük értékek megfelelő nyúlványok:

Az x, y, z koordináták a pont nevezzük MA abszcissza rendre. összehangolja és applikáta. és meg van írva egy rendezett pont számok: M (x; y; z) (6. ábra).

Egység vektor, amelynek iránya egybeesik a tengely irányában, az úgynevezett egy egységet a vektor (vagy egység vektor) tengely. Jelöljük

Ennek megfelelően, az egység vektorok a koordinátatengelyek Ox. Oy. oz

Tétel. Bármely olyan vektor lehet felbontani az egység vektorok a koordinátatengelyek:

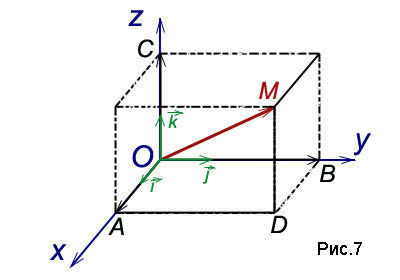
(2) egyenlet nevezzük dekompozíciós vektorok mentén koordinátatengelyek. Az együtthatók az e tágulási nyúlványok a vektor a koordinátatengelyeken. Így a tágulási tényezőjük (2) a vektor a koordinátatengelyeken a koordinátái a vektor.

Kiválasztása után egy adott térben vektor koordináta-rendszer és annak eredetét hármas egyedileg meghatározzák egymást, azonban a vektor lehet írva formájában

Vektor képviselet formájában (2) és (3) azonos.

Amint azt már említettük, a vektorokat nevezik egyenesre, amennyiben azok a

Tegyük fel, hogy a vektorok. Ezek a vektorok egy egyenesen, ha a koordinátákat a vektorok rokonságban

vagyis a koordinátákat a vektorok arányos.

4. példa Tekintettel a vektorok. hogy ezek a vektorok egy egyenesen vannak?

Határozat. Határozzuk meg az arány a koordináta adatok vektorok:

A koordinátákat a vektorok arányos, ezért a vektorok egy egyenesen vannak, vagy ami ugyanaz párhuzamos.

n - dimenziós vektorok és műveletek rájuk

A tanulmány számos kérdés, például a gazdasági, célszerű általánosítani tárgyalt technikák feltérképezése és számok között pontok kétdimenziós és háromdimenziós tér és megvizsgálja a sorozat n-es valós számok, mint a „pont” elvont „n-dimenziós tér”, és a számok önmagukban - mint " koordinálja „ezeket a pontokat. Az n-dimenziós vektor komponenseinek vehet adatokat, mint a termelékenység, különféle növények, az értékesítés volumene az áruk, a technikai tényezők, az áruk körét raktárakban, stb

n-dimenziós vektor egy rendezett halmaza n valós szám rögzített formában

ahol - i - edik elem (vagy az i - edik komponense) a x vektor.

Van még egy másik bejegyzés vektor - az oszlop formájában koordinátái:

A méret a vektor száma határozza meg annak eredetét, és ez egy sajátossága. Például, (2, 5) - dimenziós vektor (2, -3, 0) - három-dimenziós (1, 3, -2, -4, 7) - egy öt-dimenziós,

n - dimenziós vektor.

A nulla vektor, a, amelynek koordinátái mind egyenlő nullával:

Vezessük be a működését n-dimenziós vektorok.

a tényleges szám a vektoros

azaz vektor szorozni a szám minden egyes koordináta szorozni ezt a számot.

akkor kap az ellenkezője vektor

azaz hozzáadásával a vektorok az azonos méretű a megfelelő koordinátákat termwise hozzá.

Ha a cserearányok vállalkozások értékesítési hálózat értékesítési áruk meghatározott pozitív és árucikkeket az értékesítési költségek - negatív, megkapjuk a vektor-értékesítési költségek

értékesítés (költség) k - m i termékhez. és k értéke 1, 2, 3, ..., m.

A teljes költség vektor értékesítési hozzáadásával határozzák meg a vektorok y költségű értékesítési valamennyi m hálózati társaságok:

A összege szemközti vektorok ad nulla vektor:

Levonva két vektor azonos méretű a megfelelő koordinátákat kivonjuk távon távú:

Manipulálása n dimenziós vektorok megfelelnek a következő tulajdonságokkal.